9.4 Description of motion  (Page 3/4)

Experiment : motion at constant velocity

Aim:

To measure the position and time during motion at constant velocity and determine the average velocity as the gradient of a “Position vs. Time" graph.

Apparatus:

A battery operated toy car, stopwatch, meter stick or measuring tape.

Method:

1. Work with a friend. Copy the table below into your workbook.
2. Complete the table by timing the car as it travels each distance.
3. Time the car twice for each distance and take the average value as your accepted time.
4. Use the distance and average time values to plot a graph of “Distance vs. Time" onto graph paper . Stick the graph paper into your workbook. (Remember that “A vs. B" always means “y vs. x").
5. Insert all axis labels and units onto your graph.
6. Draw the best straight line through your data points.
7. Find the gradient of the straight line. This is the average velocity.

Results:

Conclusions:

Answer the following questions in your workbook.

Questions:

1. Did the car travel with a constant velocity?
2. How can you tell by looking at the “Distance vs. Time" graph if the velocity is constant?
3. How would the “Distance vs. Time" look for a car with a faster velocity?
4. How would the “Distance vs. Time" look for a car with a slower velocity?

Motion at constant acceleration

The final situation we will be studying is motion at constant acceleration. We know that acceleration is the rate of change of velocity. So, if we have a constant acceleration, this means that the velocity changes at a constant rate.

Let's look at our first example of Lesedi waiting at the taxi stop again. A taxi arrived and Lesedi got in. The taxi stopped at the stop street and then accelerated as follows: After $1s$ the taxi covered a distance of $\mathrm{2,5}m$ , after $2s$ it covered $10m$ , after $3s$ it covered $\mathrm{22,5}m$ and after $4s$ it covered $40m$ . The taxi is covering a larger distance every second. This means that it is accelerating.

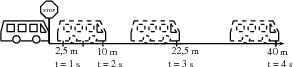
To calculate the velocity of the taxi you need to calculate the gradient of the line at each second:

From these velocities, we can draw the velocity-time graph which forms a straight line.

The acceleration is the gradient of the $v$ vs. $t$ graph and can be calculated as follows:

The acceleration does not change during the motion (the gradient stays constant). This is motion at constant or uniform acceleration.

The graphs for this situation are shown in [link] .

Velocity from acceleration vs. time graphs

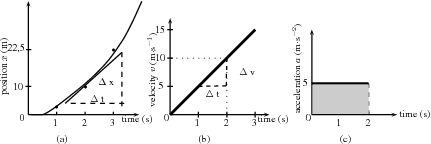
Just as we used velocity vs. time graphs to find displacement, we can use acceleration vs. time graphs to find the velocity of an object at a given moment in time. We simply calculate the area under the acceleration vs. time graph, at a given time. In the graph below, showing an object at a constant positive acceleration, the increase in velocity of the object after 2 seconds corresponds to the shaded portion.