9.4 Description of motion  (Page 2/4)

The displacement of the object is given by the area under the graph, which is $0m$ . This is obvious, because the object is not moving.

Motion at constant velocity

Motion at a constant velocity or uniform motion means that the position of the object is changing at the same rate.

Assume that Lesedi takes $100s$ to walk the $100m$ to the taxi-stop every morning. If we assume that Lesedi's house is the origin, then Lesedi's velocity is:

Lesedi's velocity is 1 m $·$ s ${}^{-1}$ . This means that he walked $1m$ in the first second, another metre in the second second, and another in the third second, and so on. For example, after $50s$ he will be $50m$ from home. His position increases by $1m$ every $1s$ . A diagram of Lesedi's position is shown in [link] .

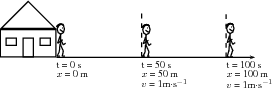
We can now draw graphs of position vs.time ( $x$ vs. $t$ ), velocity vs.time ( $v$ vs. $t$ ) and acceleration vs.time ( $a$ vs. $t$ ) for Lesedi moving at a constant velocity. The graphs are shown in [link] .

In the evening Lesedi walks $100m$ from the bus stop to his house in $100s$ . Assume that Lesedi's house is the origin. The following graphs can be drawn to describe the motion.

We see that the $v$ vs. $t$ graph is a horisontal line. If the velocity vs. time graph is a horisontal line, it means that the velocity is constant (not changing). Motion at a constant velocity is known as uniform motion .

We can use the $x$ vs. $t$ to calculate the velocity by finding the gradient of the line.

Lesedi has a velocity of $-1m·s{}^{-1}$ , or $1m·s{}^{-1}$ towards his house. You will notice that the $v$  vs.  $t$ graph is a horisontal line corresponding to a velocity of $-1m·s{}^{-1}$ . The horizontal line means that the velocity stays the same (remains constant) during the motion. This is uniform velocity.

We can use the $v$ vs. $t$ to calculate the acceleration by finding the gradient of the line.

Lesedi has an acceleration of $0m·s{}^{-2}$ . You will notice that the graph of $a$ vs. $t$ is a horisontal line corresponding to an acceleration value of $0m·s{}^{-2}$ . There is no acceleration during the motion because his velocity does not change.

We can use the $v$ vs. $t$ to calculate the displacement by finding the area under the graph.

This means that Lesedi has a displacement of $100m$ towards his house.

Velocity and acceleration

1. Use the graphs in [link] to calculate each of the following:
   1. Calculate Lesedi's velocity between $50s$ and $100s$ using the $x$ vs. $t$ graph. Hint: Find the gradient of the line.
   2. Calculate Lesedi's acceleration during the whole motion using the $v$ vs. $t$ graph.
   3. Calculate Lesedi's displacement during the whole motion using the $v$ vs. $t$ graph.
2. Thandi takes $200s$ to walk $100m$ to the bus stop every morning. In the evening Thandi takes $200s$ to walk $100m$ from the bus stop to her home.
   1. Draw a graph of Thandi's position as a function of time for the morning (assuming that Thandi's home is the reference point). Use the gradient of the $x$ vs. $t$ graph to draw the graph of velocity vs. time. Use the gradient of the $v$ vs. $t$ graph to draw the graph of acceleration vs. time.
   2. Draw a graph of Thandi's position as a function of time for the evening (assuming that Thandi's home is the origin). Use the gradient of the $x$ vs. $t$ graph to draw the graph of velocity vs. time. Use the gradient of the $v$ vs. $t$ graph to draw the graph of acceleration vs. time.
   3. Discuss the differences between the two sets of graphs in questions 2 and 3.