| << Chapter < Page | Chapter >> Page > |
The velocity of the object at is therefore . This corresponds with the values obtained in [link] .
The relation between graphs of position, velocity and acceleration as functions of time is summarised in [link] .

Often you will be required to describe the motion of an object that is presented as a graph of either position, velocity or acceleration as functions of time. The description of the motion represented by a graph should include the following (where possible):
You will also often be required to draw graphs based on a description of the motion in words or from a diagram. Remember that these are just different methods of presenting the same information. If you keep in mind the general shapes of the graphs for the different types of motion, there should not be any difficulty with explaining what is happening.
The worked examples in this section demonstrate the types of questions that can be asked about graphs.
The position vs. time graph for the motion of a car is given below. Draw the corresponding velocity vs. time and acceleration vs. time graphs, and then describe the motion of the car.

The question gives a position vs. time graph and the following three things are required:
To answer these questions, break the motion up into three sections: 0 – 2 seconds, 2 – 4 seconds and 4 – 6 seconds.
For the first 2 seconds we can see that the displacement remains constant - so the object is not moving, thus it has zero velocity during this time. We can reach this conclusion by another path too: remember that the gradient of a displacement vs. time graph is the velocity. For the first 2 seconds we can see that the displacement vs. time graph is a horizontal line, ie. it has a gradient of zero. Thus the velocity during this time is zero and the object is stationary.
For the next 2 seconds, displacement is increasing with time so the object is moving. Looking at the gradient of the displacement graph we can see that it is not constant. In fact, the slope is getting steeper (the gradient is increasing) as time goes on. Thus, remembering that the gradient of a displacement vs. time graph is the velocity, the velocity must be increasing with time during this phase.
For the final 2 seconds we see that displacement is still increasing with time, but this time the gradient is constant, so we know that the object is now travelling at a constant velocity, thus the velocity vs. time graph will be a horizontal line during this stage. We can now draw the graphs:
So our velocity vs. time graph looks like this one below. Because we haven't been given any values on the vertical axis of the displacement vs. time graph, we cannot figure out what the exact gradients are and therefore what the values of the velocities are. In this type of question it is just important to show whether velocities are positive or negative, increasing, decreasing or constant.

Once we have the velocity vs. time graph its much easier to get the acceleration vs. time graph as we know that the gradient of a velocity vs. time graph is the just the acceleration.
For the first 2 seconds the velocity vs. time graph is horisontal and has a value of zero, thus it has a gradient of zero and there is no acceleration during this time. (This makes sense because we know from the displacement time graph that the object is stationary during this time, so it can't be accelerating).
For the next 2 seconds the velocity vs. time graph has a positive gradient. This gradient is not changing (i.e. its constant) throughout these 2 seconds so there must be a constant positive acceleration.
For the final 2 seconds the object is traveling with a constant velocity. During this time the gradient of the velocity vs. time graph is once again zero, and thus the object is not accelerating. The acceleration vs. time graph looks like this:

A brief description of the motion of the object could read something like this: At s and object is stationary at some position and remains stationary until s when it begins accelerating. It accelerates in a positive direction for 2 seconds until s and then travels at a constant velocity for a further 2 seconds.
The velocity vs. time graph of a truck is plotted below. Calculate the distance and displacement of the truck after 15 seconds.

We are asked to calculate the distance and displacement of the car. All we need to remember here is that we can use the area between the velocity vs. time graph and the time axis to determine the distance and displacement.
Break the motion up: 0 – 5 seconds, 5 – 12 seconds, 12 – 14 seconds and 14 – 15 seconds.
For 0 – 5 seconds: The displacement is equal to the area of the triangle on the left:
For 12 – 14 seconds the displacement is equal to the area of the triangle above the time axis on the right:
Now the total distance of the car is the sum of all of these areas:
Now the total displacement of the car is just the sum of all of these areas. HOWEVER, because in the last second (from s to s) the velocity of the car is negative, it means that the car was going in the opposite direction, i.e. back where it came from! So, to find the total displacement, we have to add the first 3 areas (those with positive displacements) and subtract the last one (because it is a displacement in the opposite direction).
The position vs. time graph below describes the motion of an athlete.

The velocity is given by the gradient of a position vs. time graph. During the first 4 seconds, this is
For the last 3 seconds we can see that the displacement stays constant. The graph shows a horisontal line and therefore the gradient is zero. Thus .
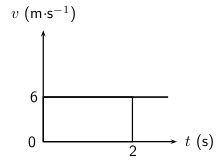
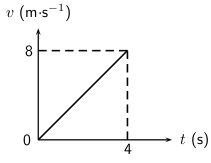
The acceleration vs. time graph for a car starting from rest, is given below. Calculate the velocity of the car and hence draw the velocity vs. time graph.

The motion of the car can be divided into three time sections: 0 – 2 seconds; 2 – 4 seconds and 4 – 6 seconds. To be able to draw the velocity vs. time graph, the velocity for each time section needs to be calculated. The velocity is equal to the area of the square under the graph:
For 0 – 2 seconds:
The velocity vs. time graph looks like this:


Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 physical science' conversation and receive update notifications?