Trình bày đại cương về lực điện động
KHÁI NIỆM CHUNG
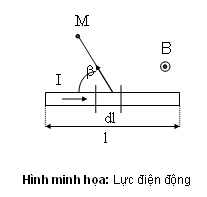
Một vật dẫn đặt trong từ trường, có dòng điện I chạy qua sẽ chịu tác động của một lực. Lực cơ học này có xu hướng làm biến dạng hoặc chuyển dời vật dẫn để từ thông xuyên qua nó là lớn nhất. Lực chuyển dời đó gọi là lực điện động. Chiều của lực điện động được xác định theo quy tắc bàn tay trái.
Ở trạng thái làm việc bình thường, thiết bị điện được chế tạo để lực điện động không làm ảnh hưởng gì đến độ bền vững kết cấu. Khi ngắn mạch dòng tăng lên rất lớn (có lúc tới hàng chục lần Iđm) do đó lực điện động sẽ rất lớn. Trong một số trường hợp dòng lớn, lực có thể tới hàng chục tấn. Lực làm biến dạng đôi khi có thể làm phá vỡ kết cấu thiết bị. Do đó cần phải nghiên cứu lực điện động để ngăn ngừa tác hại của nó khi lựa chọn, tính toán và thiết kế thiết bị điện.
Ngoài ra người ta còn nghiên cứu ứng dụng lực điện động để chế tạo các thiết bị điện như rơle điện động, cơ cấu đo điện động,...
Các phương pháp tính toán lực điện động
Phương pháp sử dụng định luật bio-xavar-laplax
Theo quan điểm của phương pháp này lực điện động là kết quả tương tác lẫn nhau của dây dẫn l mang dòng điện I và từ trường do dây dẫn khác tạo nên.
- Lực điện động tác dụng lên chiều dài l khi có dòng điện I đặt trong từ trường có từ cảm
B
→
size 12{ widevec {B} } {} là:
ΔF
→
=
I
.
Δl
→
x
ΔB
→
hay
∣
ΔF
→
∣
=
I
.
B
.
Δl
.
sin
α
size 12{ widevec {ΔF} =I "." widevec {Δl} `x` widevec {ΔB} matrix {
{} # {}} ital "hay" matrix {
{} # {}} lline widevec {ΔF} rline =I "." B "." Δl "." "sin"α} {}
Với góc là góc hợp bởi
Δl
→
size 12{ widevec {Δl} } {} và
B
→
size 12{ widevec {B} } {} (
Δl
→
size 12{ widevec {Δl} } {} cùng chiều
I
→
size 12{ widevec {I} } {} ).
là góc xác định theo chiều quay nhỏ nhất.
- Dạng vi phân là
d
F
→
=
I
.
d
l
→
x
B
→
size 12{d widevec {F} =I "." d widevec {l} `x` widevec {B} } {}
∣
d
F
→
∣
=
I
.
B
.
dl
.
sin
α
size 12{ lline d widevec {F} rline =I "." B "." ital "dl" "." "sin"α} {} (4-1)
Có :
dl
→
size 12{ {"dl"} cSup { size 8{ rightarrow } } } {} trùng chiều dòng điện i.
Từ đó ta có lực điện động :
∣
F
→
∣
=
∫
0
l
∣
d
F
→
∣
=
∫
0
l
I
.
Bdl
sin
α
size 12{ lline widevec {F} rline = Int cSub { size 8{0} } cSup { size 8{l} } { lline d widevec {F} rline } = Int cSub { size 8{0} } cSup { size 8{l} } {I "." ital "Bdl""sin"α} } {} = I.B. l.
sin
α
size 12{"sin"α} {} (4-2)
- Nếu hai dây dẫn cùng trong một mặt phẳng = 900 thì
F
=
∫
0
l
IBdl
size 12{F= Int cSub { size 8{0} } cSup { size 8{l} } { ital "IBdl"} } {} =I.B.l.
Muốn xác định được F ta phải tìm được quan hệ B = B(l), cảm ứng từ phụ thuộc kích thước dây dẫn.
- Theo Bio-Xavar-Laplax thì cường độ từ cảm tại một điểm M
B
→
size 12{ widevec {B} } {} có trị số là :
B
→
=
μ
0
4π
I
∫
d
l
→
x
r
0
→
r
2
, hay
∣
B
→
∣
=
μ
0
4π
I
∫
dl
.
sin
β
r
2
size 12{ widevec {B} = { {μ rSub { size 8{0} } } over {4π} } I Int { { {d widevec {l} `x` widevec {r rSub { size 8{0} } } } over {r rSup { size 8{2} } } } " , hay " lline widevec {B} rline = { {μ rSub { size 8{0} } } over {4π} } I Int { { { ital "dl" "." "sin"β} over {r rSup { size 8{2} } } } } } } {} (4-3)
Trong đó:
r
0
→
laì veïctå âån vë choün tæì dl âãún M coï
∣
r
0
→
∣
=
1
r
:
laì khoaíng caïch tæì dl âãún M
.
β
: goïc håüp båíi d
l
→
vaì
r
0
→
B
→
: veïc tå caím æïng tæì thàóng goïc våïi màût phàóng
do d
l
→
vaì
r
0
→
taûo lãn
.
{
{
{
{
size 12{alignl { stack {
left lbrace widevec { size 10{r rSub { size 8{0} } }} " laì veïctå âån vë choün tæì dl âãún M coï " lline size 12{ widevec {r rSub{ size 8{0} } } } rline =1 {} #
right none left lbrace size 12{r:" laì khoaíng caïch tæì dl âãún M" "." } {} #right none left lbrace size 12{β" : goïc håüp båíi d" widevec { size 12{l} } " vaì " widevec { size 12{r rSub { size 8{0} } } } } {} #
right none left lbrace size 12{ widevec {B } ": veïc tå caím æïng tæì thàóng goïc våïi màût phàóng "} {} #right none left lbrace size 12{"do d" widevec { size 12{l} } " vaì " widevec { size 12{r rSub { size 8{0} } } } " taûo lãn" "." } {} #
right no } } size 12{ lbrace }} {}
Phương pháp cân bằng năng lượng
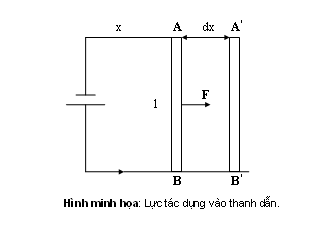
Xét một dây dẫn có dòng điện chạy qua như hình minh họa trên. Khi dây dẫn dịch chuyển theo hướng x một đoạn dx thì lực điện động được xác định bởi :
dw = F.dx
⇒
F
=
dw
dx
size 12{ drarrow matrix {
{} # F= { { ital "dw"} over { ital "dx"} } {}} } {} (4-4)
Trong đó:
+ dw : độ biến thiên năng lượng từ trường của vật dẫn mang dòng điện khi di chuyển một đoạn dx.
+ x : phương chuyển dời có thể có của dây dẫn dưới tác dụng của lực F.
+ Chiều
F
→
size 12{ widevec {F} } {} trùng với chiều dx.
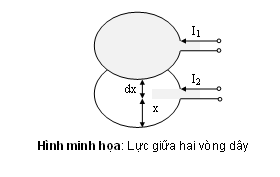
Ví dụ: xét hệ hai vật dẫn mang hai dòng điện i1 ; i2 như hình minh họa trên đặt song song cách nhau một khoảng x. Năng lượng từ trường của hệ là:
W
M
=
1
2
L
1
i
1
2
+
1
2
L
2
i
2
2
+
Mi
1
i
2
vaì
læûc taïc duûng laì :
F
=
dw
M
dx
=
d
1
2
L
1
i
1
2
+
1
2
L
2
i
2
2
+
Mi
1
i
2
dx
Ta coï læûc taïc duûng riãng reî seî laì :
F
1
=
1
2
i
1
2
.
dL
1
dx
[
J
/
cm
]
F
2
=
1
2
i
2
2
.
dL
2
dx
[
J
/
cm
]
{
alignl { stack {
{} #size 12{ size 10{W rSub { size 8{M} } = { { size 12{1} } over { size 12{2} } } L rSub { size 8{1} } i rSub { size 8{1} } rSup { size 8{2} } + { { size 12{1} } over { size 12{2} } } L rSub { size 8{2} } i rSub { size 8{2} } rSup { size 8{2} } + ital "Mi" rSub { size 8{1} } i rSub { size 8{2} } ` ital "vaì"`" læûc taïc duûng laì :"}} {} #
size 12{ size 10{F= { { size 10{"dw" rSub { size 8{M} } }} over { size 12{"dx"} } } = { { size 12{d left ( size 12{ { {1} over { size 12{2} } } L rSub { size 8{1} } i rSub { size 8{1} } rSup { size 8{2} } + { { size 12{1} } over { size 12{2} } } L rSub { size 8{2} } i rSub { size 8{2} } rSup { size 8{2} } + ital "Mi" rSub { size 8{1} } i rSub { size 8{2} } } right )} } over { size 12{ ital "dx"} } } }} {} #size 12{ size 10{"Ta coï læûc taïc duûng riãng reî seî laì :"}} {} #
size 10{ alignl { stack {left lbrace size 10{F rSub { size 8{1} } = { { size 12{1} } over { size 12{2} } } i rSub { size 8{1} } rSup { size 8{2} } "." { { size 12{ ital "dL" rSub { size 8{1} } } } over { size 12{ ital "dx"} } } \[ J/ ital "cm" \] } {} #right none left lbrace size 12{F rSub { size 8{2} } = { { size 12{1} } over { size 12{2} } } i rSub { size 8{2} } rSup { size 8{2} } "." { { size 12{ ital "dL" rSub { size 8{2} } } } over { size 12{ ital "dx"} } } \[ J/ ital "cm" \] } {} #right no } } size 12{ lbrace }} {}
} } {}