dF
x
=
−
μ
0
.
I
1
.
I
2
4π
.
x
∫
α
1
α
2
sin
α
.
dα
size 12{ ital "dF" rSub { size 8{x} } = - { {μ"" lSub { size 8{0} } "." I rSub { size 8{1} } "." I rSub { size 8{2} } } over {4π "." x} } Int cSub { size 8{α rSub { size 6{1} } } } cSup {α rSub { size 6{2} } } {"sin"α "." dα} } {} (4-13)
Lực tác dụng lên một đơn vị dài của dây l2 tại vị trí xi do
I
1
→
trong
l
1
size 12{ widevec {I rSub { size 8{1} } } ` ital "trong"`l rSub { size 8{1} } } {} gây lên là :
F
x
i
=
dF
x
i
dl
2
=
μ
0
.
I
1
.
I
2
4π
.
cos
α
2i
−
cos
α
1i
x
i
size 12{F rSub { size 8{x rSub { size 6{i} } } } = { { ital "dF" rSub {x rSub { size 6{i} } } } over { size 12{ ital "dl" rSub {2} } } } size 12{ {}= { {μ rSub {0} size 12{ "." I rSub {1} } size 12{ "." I rSub {2} }} over { size 12{4π} } } } size 12{ "." { {"cos"α rSub {2i} size 12{ - "cos"α rSub {1i} }} over { size 12{x rSub {i} } } } }} {} (4-14)
Chú ý : khi chọn các điểm tính x dọc chiều dài l2 góc và độ dài x biến thiên dẫn đến các lực Fx biến
thiên không đều dọc chiều dài l2 của dây 2.
Điểm tác dụng của lực tổng F sẽ qua trọng tâm dây l2.
Bằng phương pháp vẽ ta có thể biết sự phân bố của lực dọc chiều dài dây l2.
Lực điện động giữa hai dây dẫn đặt song song trong đó một dây dài vô tận
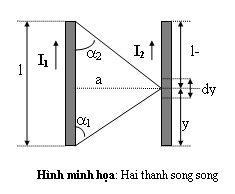
Hình minh họa, xét khi dây l1 = ; dây l2 = l khoảng cách giữa hai dây x = a. Áp dụng biểu thức (4.14) ta thay 1 = ; 2 = 0; x = a vào ta có :
F
xi
=
2μ
0
.
I
1
.
I
2
4π
.
a
=
const
size 12{F rSub { size 8{ ital "xi"} } = { {2μ rSub { size 8{0} } "." I rSub { size 8{1} } "." I rSub { size 8{2} } } over {4π "." a} } = ital "const"} {}
Lực điện động tác dụng lên dây dẫn l2 là :
F
2
=
2μ
0
.
I
1
.
I
2
4π
.
l
a
size 12{ size 10{F rSub { size 8{2} } = { { size 12{2μ rSub { size 8{0} } "." I rSub { size 8{1} } "." I rSub { size 8{2} } } } over { size 12{4π} } } "." { { size 12{l} } over { size 12{a} } } }} {} (4-14)
và có
F
2
=
0,2
.
I
1
.
I
2
.
l
a
.
10
−
8
[
J/cm
]
hay F
2
=
2,
04
.
I
1
.
I
2
.
l
a
.
10
−
8
[
kg
]
size 12{ size 10{F rSub { size 8{2} } =0,2 "." I rSub { size 8{1} } "." I rSub { size 8{2} } "." { { size 12{l} } over { size 12{a} } } "." "10" rSup { size 8{ - 8} } \[ "J/cm" \] " hay F" rSub { size 8{2} } =2,"04" "." I rSub { size 8{1} } "." I rSub { size 8{2} } "." { { size 12{l} } over { size 12{a} } } "." "10" rSup { size 8{ - 8} } \[ ital "kg" \]}} {} .
c) Lực điện động giữa hai dây dẫn song song có chiều dài bằng nhau
Áp dụng công thức (4.12) ở phần trước và thay x = a; dl2 = dy ta có :
dF
=
μ
0
.
I
1
.
I
2
4π
.
a
.
dy
(
cos
α
2
−
cos
α
1
)
size 12{ size 10{ ital "dF"= { { size 10{μ rSub { size 8{0} } "." I rSub { size 8{1} } "." I rSub { size 8{2} } }} over { size 12{4π "." a} } } "." ital "dy" \( "cos"α rSub { size 8{2} } - "cos"α rSub { size 8{1} } \) }} {} (4-15)
Trên hình 4-7 có :
cos
α
2
=
l
−
y
(
l
−
y
)
2
+
a
2
,coìn
cos
α
1
=
−
cos
(
π
−
α
1
)
=
y
y
2
+
a
2
size 12{"cos"α rSub { size 8{2} } = { {l - y} over { \( l - y \) rSup { size 8{2} } +a rSup { size 8{2} } } } " ,coìn "`"cos"α rSub { size 8{1} } = - "cos" \( π - α rSub { size 8{1} } \) = { {y} over { sqrt {y rSup { size 8{2} } +a rSup { size 8{2} } } } } } {}
Vậy :
F
=
μ
0
.
I
1
.
I
2
4π
.
a
∫
0
l
(
l
−
y
)
dy
(
l
−
y
)
2
+
a
2
+
∫
0
l
ydy
y
2
+
a
2
size 12{ size 10{F= { { size 10{μ rSub { size 8{0} } "." I rSub { size 8{1} } "." I rSub { size 8{2} } }} over { size 12{4π "." a} } } left [ size 12{ Int cSub { size 8{0} } cSup { size 8{l} } { { { \( l - y \) ital "dy"} over { size 12{ sqrt { \( l - y \) rSup { size 8{2} } +a rSup { size 8{2} } } } } } +{}} Int cSub { size 8{0} } cSup { size 8{l} } { size 12{ { { ital "ydy"} over { size 12{ sqrt {y rSup { size 8{2} } +a rSup { size 8{2} } } } } } } } } right ]}} {} (4-16)
Tính từng tích phân riêng rẽ có :
A
=
∫
0
l
ydy
y
2
+
a
2
size 12{ size 10{A= Int cSub { size 8{0} } cSup { size 8{l} } { { { size 10{ ital "ydy"}} over { sqrt { size 10{y rSup { size 8{2} } +a rSup { size 8{2} } }} } } } }} {}
Nếu đặt z2= y2+a2
⇒
size 12{ drarrow } {} 2zdz = 2ydy và:
+ khi y= 0 thì z= a
+khi y=1 thì z=
l
2
+
a
2
size 12{ sqrt {l rSup { size 8{2} } +a rSup { size 8{2} } } } {}
{}
{}
đổi cận ta có :
A
=
∫
0
l
ydy
y
2
+
a
2
=
∫
a
l
2
+
a
2
dz
=
a
2
+
l
2
−
a
.
size 12{ size 10{A= Int cSub { size 8{0} } cSup { size 8{l} } { { { size 10{ ital "ydy"}} over { sqrt { size 10{y rSup { size 8{2} } +a rSup { size 8{2} } }} } } } = Int cSub { size 8{a} } cSup { size 8{ sqrt {l rSup { size 6{2} } +a rSup { size 6{2} } } } } { size 12{ ital "dz"} } = sqrt { size 12{a rSup { size 8{2} } +l rSup { size 8{2} } } } - a "." }} {}
∫
0
l
(
l
−
y
)
dy
(
l
−
y
)
2
+
a
2
=
−
∫
l
0
udu
u
2
+
a
2
=
l
2
+
a
2
−
a
size 12{ Int cSub { size 8{0} } cSup { size 8{l} } { { { size 10{ \( l - y \) ital "dy"}} over { sqrt { size 10{ \( l - y \) rSup { size 8{2} } +a rSup { size 8{2} } }} } } } =- Int cSub { size 8{l} } cSup { size 8{0} } { size 12{ { { ital "udu"} over { size 12{ sqrt {u rSup { size 8{2} } +a rSup { size 8{2} } } } } } } } = sqrt { size 12{l rSup { size 8{2} } +a rSup { size 8{2} } } } - a} {}
Đổ̉i cận ta có:
F
=
μ
0
.
I
1
.
I
2
4π
.
a
.
2
a
2
+
l
2
−
a
=
μ
0
.
I
1
.
I
2
2π
.
l
a
2
1
+
a
2
l
2
−
a
l
size 12{ size 10{F= { { size 10{μ rSub { size 8{0} } "." I rSub { size 8{1} } "." I rSub { size 8{2} } }} over { size 12{4π "." a} } } "." 2 left ( size 12{ sqrt {a rSup { size 8{2} } +l rSup { size 8{2} } } - a} right )= { { size 12{μ rSub { size 8{0} } "." I rSub { size 8{1} } "." I rSub { size 8{2} } } } over { size 12{2π} } } "." { { size 12{l} } over { size 12{a rSup { size 8{2} } } } } left [ size 12{ sqrt {1+ { { size 12{a rSup { size 8{2} } } } over { size 12{l rSup { size 8{2} } } } } } - { { size 12{a} } over { size 12{l} } } } right ]}} {}
Từ đó thay vào (4.16) ta có :
ϕ
(
a
l
)
=
1
+
a
2
l
2
−
a
l
hay coìn goüi haìm hiãûu chènh khi l
>>
a thç
ϕ
(
a
l
)
≈
1
coï :
size 12{ size 10{ϕ \( { { size 10{a}} over { size 10{l}} } \) = sqrt { size 10{1+ { { size 10{a rSup { size 8{2} } }} over { size 12{l rSup { size 8{2} } } } } }} - { { size 12{a} } over { size 12{l} } } " hay coìn goüi haìm hiãûu chènh khi l"">>""a thç "ϕ \( { { size 12{a} } over { size 12{l} } } \) approx 1" coï :"}} {}
đặt
F
=
0,2
I
1
.
I
2
.
l
a
.
ϕ
(
a
l
)
.
10
−
8
[
J
/
cm
]
hay:
F
=
2,
04
.
I
1
.
I
2
.
l
a
.
ϕ
(
a
l
)
.
10
−
8
[
kg
]
size 12{ size 10{F=0,2I rSub { size 8{1} } "." I rSub { size 8{2} } "." { { size 12{l} } over { size 12{a} } } "." ϕ \( { { size 12{a} } over { size 12{l} } } \) "." "10" rSup { size 8{ - 8} } \[ J/ ital "cm" \] `"hay: "F=2,"04" "." I rSub { size 8{1} } "." I rSub { size 8{2} } "." { { size 12{l} } over { size 12{a} } } "." ϕ \( { { size 12{a} } over { size 12{l} } } \) "." "10" rSup { size 8{ - 8} } \[ ital "kg" \]}} {}
F
=
0,2
I
1
I
2
l
.
1
h
2
2h
a
arctg
h
a
−
ln
l
+
h
2
a
2
.
10
−
8
[
J
/
cm
]
size 12{ size 10{F=0,2I rSub { size 8{1} } I rSub { size 8{2} } l "." { { size 12{1} } over { size 12{h rSup { size 8{2} } } } } left [ size 12{ { {2h} over { size 12{a} } } ital "arctg" { { size 12{h} } over { size 12{a} } } - "ln" left ( size 12{l+ { { size 12{h rSup { size 8{2} } } } over { size 12{a rSup { size 8{2} } } } } } right )} right ] "." "10" rSup { size 8{ - 8} } \[ J/ ital "cm" \]}} {}
Khi hai thanh dẫn có tiết diện chữ nhật với kích thước rộng b, cao h và dài l
+ Nếu có b h, b a thì :
F
=
0,2
.
I
1
I
2
l
a
.
10
−
8
ϕ
(
f
)
[
J
/
cm
]
size 12{ size 10{F=0,2 "." I rSub { size 8{1} } I rSub { size 8{2} } { { size 12{l} } over { size 12{a} } } "." "10" rSup { size 8{ - 8} } ϕ \( f \) ~` \[ J/ ital "cm" \] }} {} . Có thể viết dưới dạng :
F
=
2,
04
.
I
1
I
2
l
a
.
10
−
8
ϕ
(
f
)
[
kg
]
size 12{ size 10{F=2,"04" "." I rSub { size 8{1} } I rSub { size 8{2} } { { size 12{l} } over { size 12{a} } } "." "10" rSup { size 8{ - 8} } ϕ \( f \) ~` \[ ital "kg" \] }} {} hay
j
size 12{j} {}
có
h
a
;
a
−
b
h
+
b
size 12{ { { size 10{h}} over { size 10{a}} } ;~ { { size 10{a - b}} over { size 10{h+b}} } } {} (f) gọi là hàm Dwight phụ thuộc theo
{}
F
=
2,
04
.
I
1
I
2
l
a
.
10
−
8
ϕ
(
f
)
[
kg
]
size 12{ size 10{F=2,"04" "." I rSub { size 8{1} } I rSub { size 8{2} } { { size 12{l} } over { size 12{a} } } "." "10" rSup { size 8{ - 8} } ϕ \( f \) ~` \[ ital "kg" \] }} {}
+ Nếu h<<a ; h/b<1 thì:
ϕ
(
f
)
=
a
2
b
2
[
(
1
+
a
b
)
+
(
1
−
b
a
)
.
ln
(
1
−
b
a
)
]
size 12{ size 10{ϕ \( f \) `= { { size 10{a rSup { size 8{2} } }} over { size 12{b rSup { size 8{2} } } } } \[ \( 1+ { { size 12{a} } over { size 12{b} } } \) + \( 1 - { { size 12{b} } over { size 12{a} } } \) "." "ln" \( 1 - { { size 12{b} } over { size 12{a} } } \) \]}} {}
Trong đó :
2
size 12{ sqrt {2} } {} .
Lực điện động trong mạch điện xoay chiều
Mạch xoay chiều một pha
Xét hai dây dẫn song song có hai dòng điện i1, i2 cùng pha (hoặc lệch một góc ) giả thiết i1 = i2 = Imsint = I
F
=
C
.
I
m
2
.
sin
2
ω
.
t
=
C
.
I
m
2
.
1
−
cos
2ω
.
t
2
=
C
.
I
m
2
2
−
C
.
I
m
2
.
cos
2ω
.
t
2
=
F
1
+
F
2
size 12{ size 10{F=C "." I rSub { size 8{m} } rSup { size 8{2} } "." "sin" rSup { size 8{2} } ω "." t=C "." I rSub { size 8{m} } rSup { size 8{2} } "." { { size 12{1 - "cos"2ω "." t} } over { size 12{2} } } = { { size 12{C "." I rSub { size 8{m} } rSup { size 8{2} } } } over { size 12{2} } } - { { size 12{C "." I rSub { size 8{m} } rSup { size 8{2} } "." "cos"2ω "." t} } over { size 12{2} } } =F rSub { size 8{1} } +F rSub { size 8{2} } }} {} sint = i
Lực điện động F = C.i2 , với C là hằng số :
Hình 4-8: Lực điện động trong mạch một pha
F
1
=
CI
m
2
2
size 12{ size 10{F rSub { size 8{1} } = { { size 12{ ital "CI" rSub { size 8{m} } rSup { size 8{2} } } } over { size 12{2} } } }} {}
Trong đó :
F
2
=
−
CI
m
2
.
cos
2ωt
2
=
−
F
1
cos
2ωt
size 12{ size 10{F rSub { size 8{2} } = - { { size 12{ ital "CI" rSub { size 8{m} } rSup { size 8{2} } "." "cos"2ωt} } over { size 12{2} } } = - F rSub { size 8{1} } "cos"2ωt}} {} là thành phần không đổi.
F
tb
=
C
.
I
m
2
2
=
CI
2
size 12{ size 10{F rSub { size 8{ ital "tb"} } = { { size 12{C "." I rSub { size 8{m} } rSup { size 8{2} } } } over { size 12{2} } } = ital "CI" rSup { size 8{2} } }} {} là
thành phần lực thay đổi.
Ta biểu diễn như hình 4-8 :
Lực F biến thiên khoảng từ 0 đến CIm2.
- Lực trung bình
i
=
2
.
I
e
−
t
T
−
cos
ωt
size 12{ size 10{i= sqrt { size 10{2}} "." I left ( size 10{e rSup { size 8{ - { { size 8{t} } over { size 8{T} } } } } - "cos"ωt} right )}} {}
Khi xảy ra ngắn mạch lực F rất lớn, dòng điện
λ
=
1
T
size 12{ size 10{λ= { { size 10{1}} over { size 10{T}} } }} {}
Hình 4-9: Lực điện động khi ngắn mạchĐặt
λ
=
22
size 12{λ="22"} {} là hệ số cản của dòng không tuần hoàn, phụ thuộc vào máy phát điện và các thông số của mạch điện. Theo thí nghiệm có
F
=
Ci
2
=
2
CI
2
(
e
−
λt
−
cos
ωt
)
2
size 12{ size 10{F= ital "Ci" rSup { size 8{2} } =2 ital "CI" rSup { size 8{2} } \( e rSup { size 8{ - λt} } - "cos"ωt \) rSup { size 8{2} } }} {} , ta có lực điện động là:
2
size 12{ sqrt {2} } {}
Tức là trong mạch gồm hai thành phần là thành phần biến đổi tuần hoàn và thành phần không tuần hoàn. Sau một số chu kì (nT) thành phần không tuần hoàn suy giảm về 0, do đó lực ổn định (một số nửa chu kì đỉnh nhọn thấp dần, một số nửa cao dần đến bằng nhau và ổn định như hình 4-9).