| << Chapter < Page | Chapter >> Page > |
The most efficient way for equal sized spheres to be packed in three dimensions is to stack close packed layers on top of each other to give a close packed structure. There are two simple ways in which this can be done, resulting in either a hexagonal or cubic close packed structures.
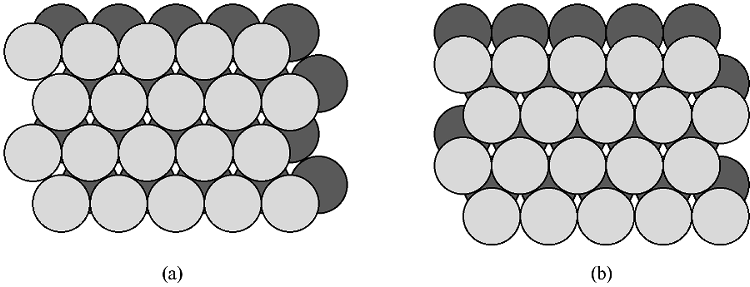
If two close packed layers A and B are placed in contact with each other so as to maximize the density, then the spheres of layer B will rest in the hollow (vacancy) between three of the spheres in layer A. This is demonstrated in [link] . Atoms in the second layer, B (shaded light gray), may occupy one of two possible positions ( [link] a or b) but not both together or a mixture of each. If a third layer is placed on top of layer B such that it exactly covers layer A, subsequent placement of layers will result in the following sequence ...ABABAB.... This is known as hexagonal close packing or hcp .
The hexagonal close packed cell is a derivative of the hexagonal Bravais lattice system ( [link] ) with the addition of an atom inside the unit cell at the coordinates ( 1 / 3 , 2 / 3 , 1 / 2 ). The basal plane of the unit cell coincides with the close packed layers ( [link] ). In other words the close packed layer makes-up the {001} family of crystal planes.
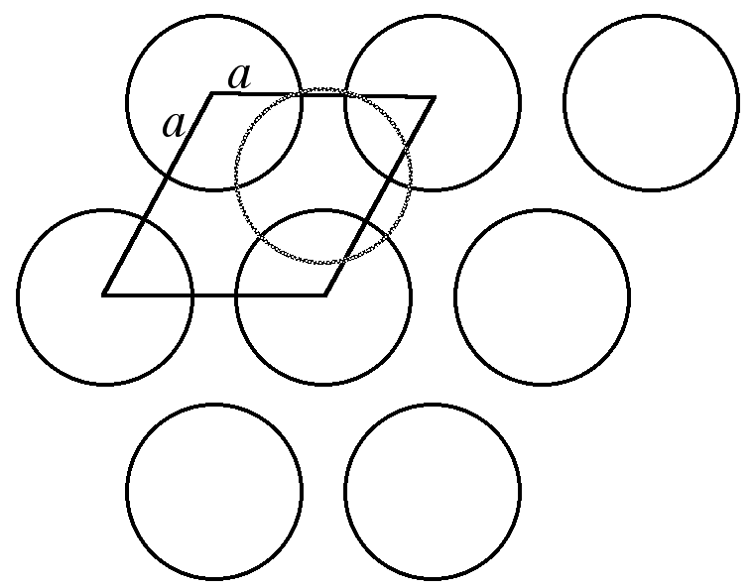
The “packing fraction” in a hexagonal close packed cell is 74.05%; that is 74.05% of the total volume is occupied. The packing fraction or density is derived by assuming that each atom is a hard sphere in contact with its nearest neighbors. Determination of the packing fraction is accomplished by calculating the number of whole spheres per unit cell (2 in hcp), the volume occupied by these spheres, and a comparison with the total volume of a unit cell. The number gives an idea of how “open” or filled a structure is. By comparison, the packing fraction for body-centered cubic ( [link] ) is 68% and for diamond cubic (an important semiconductor structure to be described later) is it 34%.
In a similar manner to the generation of the hexagonal close packed structure, two close packed layers are stacked ( [link] ) however, the third layer (C) is placed such that it does not exactly cover layer A, while sitting in a set of troughs in layer B ( [link] ), then upon repetition the packing sequence will be ...ABCABCABC.... This is known as cubic close packing or ccp .

The unit cell of cubic close packed structure is actually that of a face-centered cubic ( fcc ) Bravais lattice. In the fcc lattice the close packed layers constitute the {111} planes. As with the hcp lattice packing fraction in a cubic close packed ( fcc ) cell is 74.05%. Since face centered cubic or fcc is more commonly used in preference to cubic close packed ( ccp ) in describing the structures, the former will be used throughout this text.

Notification Switch
Would you like to follow the 'Chemistry of electronic materials' conversation and receive update notifications?