| << Chapter < Page | Chapter >> Page > |
Let’s consider the number The real part of the complex number is and the imaginary part is 3. We plot the ordered pair to represent the complex number as shown in [link] .
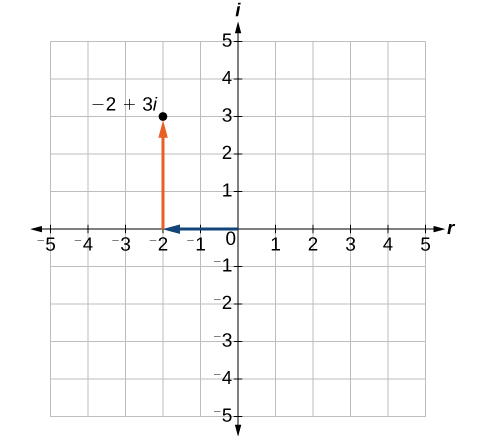
In the complex plane, the horizontal axis is the real axis, and the vertical axis is the imaginary axis, as shown in [link] .
Given a complex number, represent its components on the complex plane.
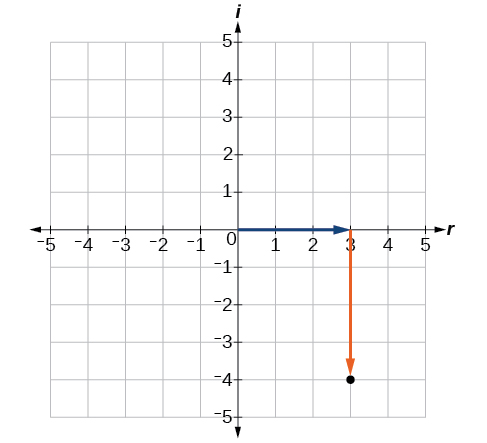
Plot the complex number on the complex plane.
The real part of the complex number is and the imaginary part is –4. We plot the ordered pair as shown in [link] .
Just as with real numbers, we can perform arithmetic operations on complex numbers. To add or subtract complex numbers, we combine the real parts and then combine the imaginary parts.
Adding complex numbers:
Subtracting complex numbers:
Given two complex numbers, find the sum or difference.
Add or subtract as indicated.
We add the real parts and add the imaginary parts.
Multiplying complex numbers is much like multiplying binomials. The major difference is that we work with the real and imaginary parts separately.
Lets begin by multiplying a complex number by a real number. We distribute the real number just as we would with a binomial. Consider, for example, :
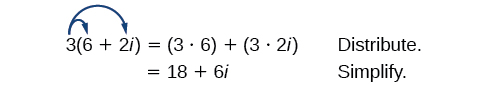
Given a complex number and a real number, multiply to find the product.
Find the product
Distribute the 4.
Now, let’s multiply two complex numbers. We can use either the distributive property or more specifically the FOIL method because we are dealing with binomials. Recall that FOIL is an acronym for multiplying First, Inner, Outer, and Last terms together. The difference with complex numbers is that when we get a squared term, it equals
Given two complex numbers, multiply to find the product.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?