6.3 Bohr’s theory of the hydrogen atom  (Page 4/14)

where $L$ is the angular momentum, $m_e$ is the electron’s mass, $r_n$ is the radius of the $n$ th orbit, and $h$ is Planck’s constant. Note that angular momentum is $L=\mathrm{I\omega }$ . For a small object at a radius $r,I={\text{mr}}^2$ and $\omega =v/r$ , so that $L=\left({\text{mr}}^2\right)\left(v/r\right)=\text{mvr}$ . Quantization says that this value of $\text{mvr}$ can only be equal to $h/\mathrm{2,}2h/\mathrm{2,}3h/2$ , etc. At the time, Bohr himself did not know why angular momentum should be quantized, but using this assumption he was able to calculate the energies in the hydrogen spectrum, something no one else had done at the time.

From Bohr’s assumptions, we will now derive a number of important properties of the hydrogen atom from the classical physics we have covered in the text. We start by noting the centripetal force causing the electron to follow a circular path is supplied by the Coulomb force. To be more general, we note that this analysis is valid for any single-electron atom. So, if a nucleus has $Z$ protons ( $Z=1$ for hydrogen, 2 for helium, etc.) and only one electron, that atom is called a hydrogen-like atom    . The spectra of hydrogen-like ions are similar to hydrogen, but shifted to higher energy by the greater attractive force between the electron and nucleus. The magnitude of the centripetal force is $m_e{v}^2/r_n$ , while the Coulomb force is $k\left({\text{Zq}}_e\right)\left(q_e\right)/r_n^2$ . The tacit assumption here is that the nucleus is more massive than the stationary electron, and the electron orbits about it. This is consistent with the planetary model of the atom. Equating these,

Angular momentum quantization is stated in an earlier equation. We solve that equation for $v$ , substitute it into the above, and rearrange the expression to obtain the radius of the orbit. This yields:

where $a_{\text{B}}$ is defined to be the Bohr radius    , since for the lowest orbit $\left(n=1\right)$ and for hydrogen $\left(Z=1\right)$ , $r_1=a_{\text{B}}$ . It is left for this chapter’s Problems and Exercises to show that the Bohr radius is

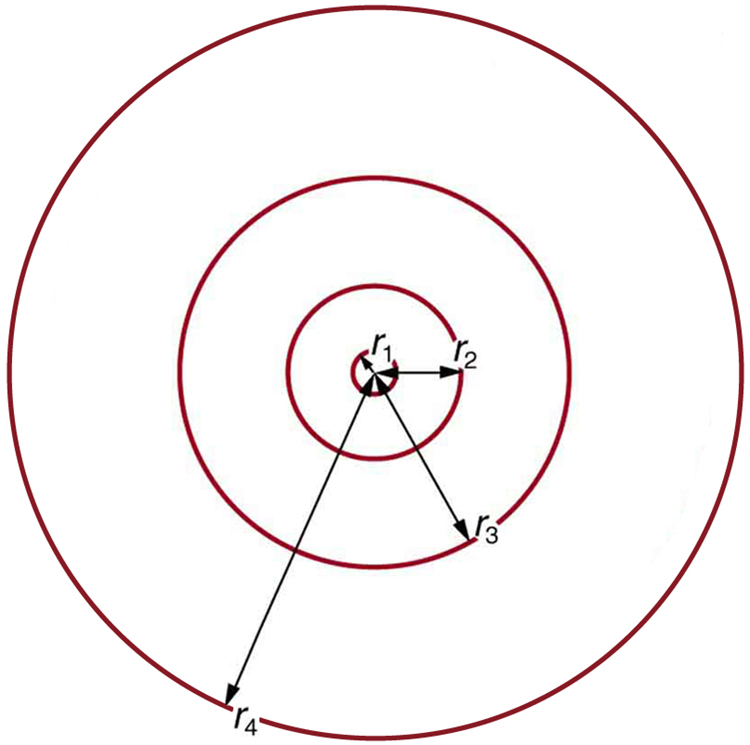
These last two equations can be used to calculate the radii of the allowed (quantized) electron orbits in any hydrogen-like atom . It is impressive that the formula gives the correct size of hydrogen, which is measured experimentally to be very close to the Bohr radius. The earlier equation also tells us that the orbital radius is proportional to $n^2$ , as illustrated in [link] .

To get the electron orbital energies, we start by noting that the electron energy is the sum of its kinetic and potential energy:

Kinetic energy is the familiar $\text{KE}=\left(1/2\right)m_e{v}^2$ , assuming the electron is not moving at relativistic speeds. Potential energy for the electron is electrical, or $\text{PE}=q_{e}V$ , where $V$ is the potential due to the nucleus, which looks like a point charge. The nucleus has a positive charge ${\text{Zq}}_e$ ; thus, $V={\text{kZq}}_e/r_n$ , recalling an earlier equation for the potential due to a point charge. Since the electron’s charge is negative, we see that $\text{PE}=-{\text{kZq}}_e/r_n$ . Entering the expressions for $\text{KE}$ and $\text{PE}$ , we find