| << Chapter < Page | Chapter >> Page > |
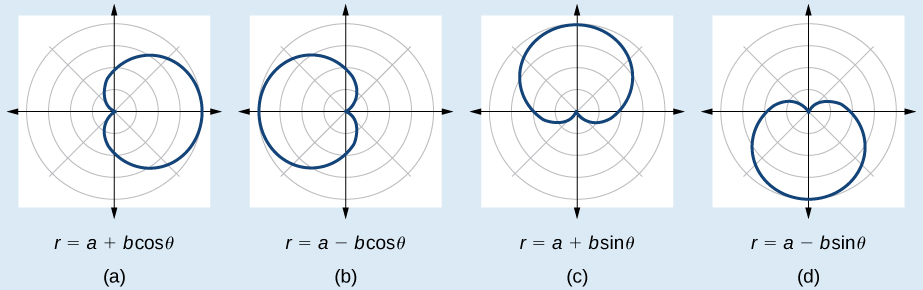
The formulas that produce the graphs of a cardioid are given by and where and The cardioid graph passes through the pole, as we can see in [link] .
Given the polar equation of a cardioid, sketch its graph.
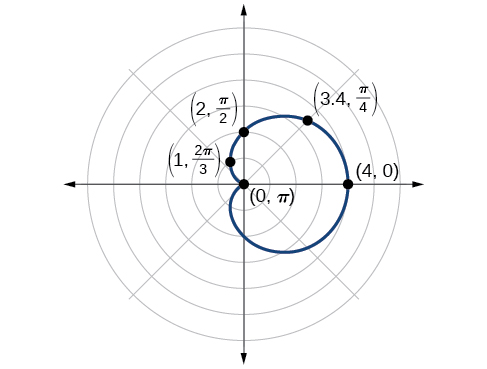
Sketch the graph of
First, testing the equation for symmetry, we find that the graph of this equation will be symmetric about the polar axis. Next, we find the zeros and maximums. Setting we have The zero of the equation is located at The graph passes through this point.
The maximum value of occurs when is a maximum, which is when or when Substitute into the equation, and solve for
The point is the maximum value on the graph.
We found that the polar equation is symmetric with respect to the polar axis, but as it extends to all four quadrants, we need to plot values over the interval The upper portion of the graph is then reflected over the polar axis. Next, we make a table of values, as in [link] , and then we plot the points and draw the graph. See [link] .
| 4 | 3.41 | 2 | 1 | 0 |
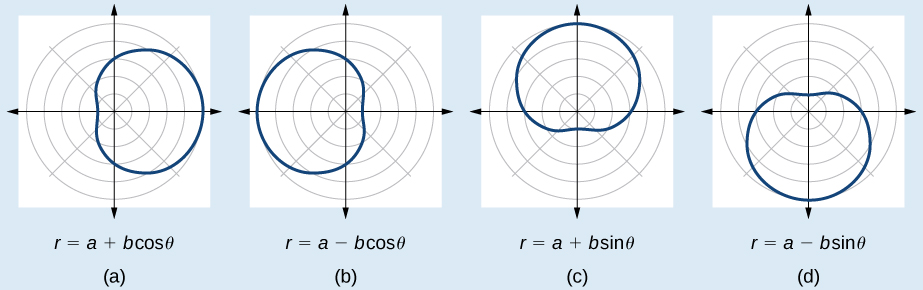
The word limaçon is Old French for “snail,” a name that describes the shape of the graph. As mentioned earlier, the cardioid is a member of the limaçon family, and we can see the similarities in the graphs. The other images in this category include the one-loop limaçon and the two-loop (or inner-loop) limaçon. One-loop limaçons are sometimes referred to as dimpled limaçons when and convex limaçons when
The formulas that produce the graph of a dimpled one-loop limaçon are given by and where All four graphs are shown in [link] .
Given a polar equation for a one-loop limaçon, sketch the graph.
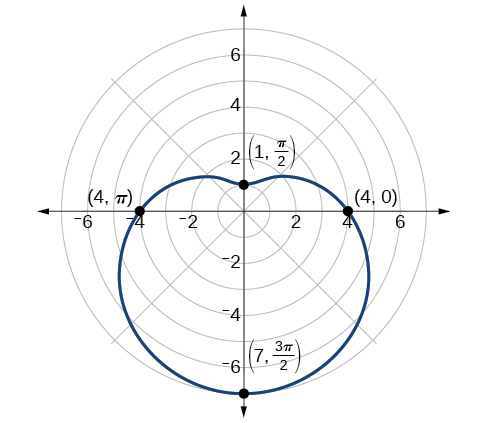
Graph the equation
First, testing the equation for symmetry, we find that it fails all three symmetry tests, meaning that the graph may or may not exhibit symmetry, so we cannot use the symmetry to help us graph it. However, this equation has a graph that clearly displays symmetry with respect to the line yet it fails all the three symmetry tests. A graphing calculator will immediately illustrate the graph’s reflective quality.
Next, we find the zeros and maximum, and plot the reflecting points to verify any symmetry. Setting results in being undefined. What does this mean? How could be undefined? The angle is undefined for any value of Therefore, is undefined because there is no value of for which Consequently, the graph does not pass through the pole. Perhaps the graph does cross the polar axis, but not at the pole. We can investigate other intercepts by calculating when
So, there is at least one polar axis intercept at
Next, as the maximum value of the sine function is 1 when we will substitute into the equation and solve for Thus,
Make a table of the coordinates similar to [link] .
| 4 | 2.5 | 1.4 | 1 | 1.4 | 2.5 | 4 | 5.5 | 6.6 | 7 | 6.6 | 5.5 | 4 |
The graph is shown in [link] .

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?