| << Chapter < Page | Chapter >> Page > |
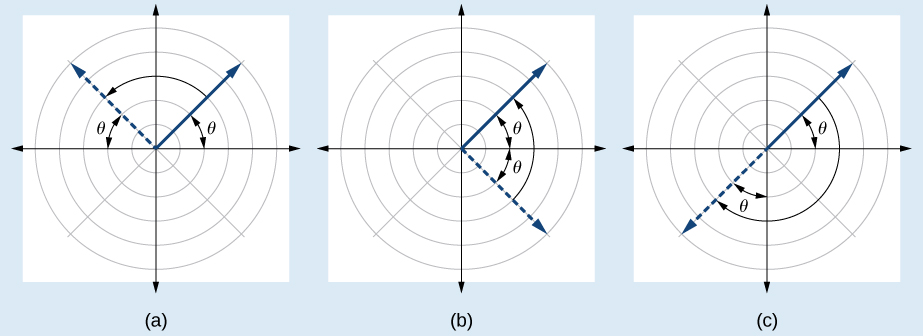
A polar equation describes a curve on the polar grid. The graph of a polar equation can be evaluated for three types of symmetry, as shown in [link] .
Given a polar equation, test for symmetry.
Test the equation for symmetry.
Test for each of the three types of symmetry.
| 1) Replacing with yields the same result. Thus, the graph is symmetric with respect to the line | |
| 2) Replacing with does not yield the same equation. Therefore, the graph fails the test and may or may not be symmetric with respect to the polar axis. | |
| 3) Replacing with changes the equation and fails the test. The graph may or may not be symmetric with respect to the pole. |
Test the equation for symmetry:
The equation fails the symmetry test with respect to the line and with respect to the pole. It passes the polar axis symmetry test.
To graph in the rectangular coordinate system we construct a table of and values. To graph in the polar coordinate system we construct a table of and values. We enter values of into a polar equation and calculate However, using the properties of symmetry and finding key values of and means fewer calculations will be needed.
To find the zeros of a polar equation, we solve for the values of that result in Recall that, to find the zeros of polynomial functions, we set the equation equal to zero and then solve for We use the same process for polar equations. Set and solve for
For many of the forms we will encounter, the maximum value of a polar equation is found by substituting those values of into the equation that result in the maximum value of the trigonometric functions. Consider the maximum distance between the curve and the pole is 5 units. The maximum value of the cosine function is 1 when so our polar equation is and the value will yield the maximum
Similarly, the maximum value of the sine function is 1 when and if our polar equation is the value will yield the maximum We may find additional information by calculating values of when These points would be polar axis intercepts, which may be helpful in drawing the graph and identifying the curve of a polar equation.

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?