| << Chapter < Page | Chapter >> Page > |
Các giới hạn của đa năng hóa toán tử:
Chúng ta không thể định nghĩa các toán tử mới.
Hầu hết các toán tử của C++ đều có thể được đa năng hóa. Các toán tử sau không được đa năng hóa là :
| Toán tử | Ý nghĩa |
| :: | Toán tử định phạm vi. |
| .* | Truy cập đến con trỏ là trường của struct hay thành viên của class. |
| . | Truy cập đến trường của struct hay thành viên của class. |
| ?: | Toán tử điều kiện |
| sizeof |
và chúng ta cũng không thể đa năng hóa bất kỳ ký hiệu tiền xử lý nào.
Chúng ta không thể thay đổi thứ tự ưu tiên của một toán tử hay không thể thay đổi số các toán hạng của nó.
Chúng ta không thể thay đổi ý nghĩa của các toán tử khi áp dụng cho các kiểu có sẵn.
Đa năng hóa các toán tử không thể có các tham số có giá trị mặc định.
Các toán tử có thể đa năng hoá:
| + | - | * | / | % | ^ |
| ! | = | < | > | += | -= |
| ^= | &= | |= | << | >> | <<= |
| <= | >= | && | || | ++ | -- |
| () | [] | new | delete | & | | |
| ~ | *= | /= | %= | >>= | == |
| != | , | -> | ->* |
Các toán tử được phân loại như sau :
Các toán tử một ngôi : *&~ ! ++ -- sizeof (data_type)
Các toán tử này được định nghĩa chỉ có một tham số và phải trả về một giá trị cùng kiểu với tham số của chúng. Đối với toán tử sizeof phải trả về một giá trị kiểu size_t (định nghĩa trong stddef.h)
Toán tử (data_type) được dùng để chuyển đổi kiểu, nó phải trả về một giá trị có kiểu là data_type.
Các toán tử hai ngôi: * / % + ->><<><
>=<= == !=&| ^&&||
Các toán tử này được định nghĩa có hai tham số.
Các phép gán: = += -= *= /= %=>>=<<= ^= |=
Các toán tử gán được định nghĩa chỉ có một tham số. Không có giới hạn về kiểu của tham số và kiểu trả về của phép gán.
Toán tử lấy thành viên : ->
Toán tử lấy phần tử theo chỉ số: []
Toán tử gọi hàm: ()
![]() Bài 1: Hãy viết lại chương trình sau bằng cách sử dụng lại các dòng nhập/xuất trong C++.
Bài 1: Hãy viết lại chương trình sau bằng cách sử dụng lại các dòng nhập/xuất trong C++.
/* Chương trình tìm mẫu chung nhỏ nhất */
#include<stdio.h>
int main()
{
int a,b,i,min;
printf("Nhap vao hai so:");
scanf("%d%d",&a,&b);
min=a>b?b:a;
for(i = 2;i<min;++i)
if (((a%i)==0)&&((b%i)==0)) break;
if(i==min) {
printf("Khong co mau chung nho nhat");
return 0;
}
printf("Mau chung nho nhat la %d\n",i);
return 0;
}
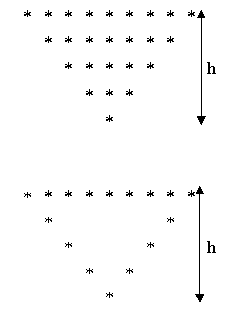
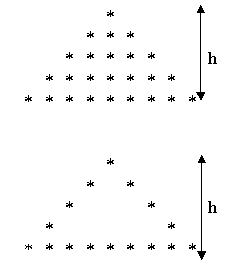
![]() Bài 2: Viết chương trình nhập vào số nguyên dương h (2<h<23), sau đó in ra các tam giác có chiều cao là h như các hình sau:
Bài 2: Viết chương trình nhập vào số nguyên dương h (2<h<23), sau đó in ra các tam giác có chiều cao là h như các hình sau:
![]() Bài 3: Một tam giác vuông có thể có tất cả các cạnh là các số nguyên. Tập của ba số nguyên của các cạnh của một tam giác vuông được gọi là bộ ba Pitago. Đó là tổng bình phương của hai cạnh bằng bình phương của cạnh huyền, chẳng hạn bộ ba Pitago (3, 4, 5). Viết chương trình tìm tất cả các bộ ba Pitago như thế sao cho tất cả các cạnh không quá 500.
Bài 3: Một tam giác vuông có thể có tất cả các cạnh là các số nguyên. Tập của ba số nguyên của các cạnh của một tam giác vuông được gọi là bộ ba Pitago. Đó là tổng bình phương của hai cạnh bằng bình phương của cạnh huyền, chẳng hạn bộ ba Pitago (3, 4, 5). Viết chương trình tìm tất cả các bộ ba Pitago như thế sao cho tất cả các cạnh không quá 500.
![]() Bài 4: Viết chương trình in bảng của các số từ 1 đến 256 dưới dạng nhị phân, bát phân và thập lục phân tương ứng.
Bài 4: Viết chương trình in bảng của các số từ 1 đến 256 dưới dạng nhị phân, bát phân và thập lục phân tương ứng.
![]() Bài 5: Viết chương trình nhập vào một số nguyên dương n. Kiểm tra xem số nguyên n có thuộc dãy Fibonacci không?
Bài 5: Viết chương trình nhập vào một số nguyên dương n. Kiểm tra xem số nguyên n có thuộc dãy Fibonacci không?
![]() Bài 6: Viết chương trình nhân hai ma trân Amxn và Bnxp. Mỗi ma trận được cấp phát động và các giá trị của chúng phát sinh ngẫu nhiên (Với m, n và p nhập từ bàn phím).
Bài 6: Viết chương trình nhân hai ma trân Amxn và Bnxp. Mỗi ma trận được cấp phát động và các giá trị của chúng phát sinh ngẫu nhiên (Với m, n và p nhập từ bàn phím).
![]() Bài 7: Viết chương trình tạo một mảng một chiều động có kích thước là n (n nhập từ bàn phím). Các giá trị của mảng này được phát sinh ngẫu nhiên trên đoạn [a, b] với a và b đều nhập từ bàn phím. Hãy tìm số dương nhỏ nhất và số âm lớn nhất trong mảng; nếu không có số dương nhỏ nhất hoặc số âm lớn nhất thì xuất thông báo "không có số dương nhỏ nhất" hoặc "không có số âm lớn nhất".
Bài 7: Viết chương trình tạo một mảng một chiều động có kích thước là n (n nhập từ bàn phím). Các giá trị của mảng này được phát sinh ngẫu nhiên trên đoạn [a, b] với a và b đều nhập từ bàn phím. Hãy tìm số dương nhỏ nhất và số âm lớn nhất trong mảng; nếu không có số dương nhỏ nhất hoặc số âm lớn nhất thì xuất thông báo "không có số dương nhỏ nhất" hoặc "không có số âm lớn nhất".
![]() Bài 8: Anh (chị) hãy viết một hàm tính bình phương của một số. Hàm sẽ trả về giá trị bình phương của tham số và có kiểu cùng kiểu với tham số.
Bài 8: Anh (chị) hãy viết một hàm tính bình phương của một số. Hàm sẽ trả về giá trị bình phương của tham số và có kiểu cùng kiểu với tham số.
![]() Bài 9: Trong ngôn ngữ C, chúng ta có hàm chuyển đổi một chuỗi sang số, tùy thuộc vào dạng của chuỗi chúng ta có các hàm chuyển đổi sau :
Bài 9: Trong ngôn ngữ C, chúng ta có hàm chuyển đổi một chuỗi sang số, tùy thuộc vào dạng của chuỗi chúng ta có các hàm chuyển đổi sau :

Chuyển đổi một chuỗi s thành số nguyên kiểu int.

Chuyển đổi một chuỗi s thành số nguyên kiểu long.

Chuyển đổi một chuỗi s thành số thực kiểu double.
Anh (chị) hãy viết một hàm có tên là aton (ascii to number) để chuyển đổi chuỗi sang các dạng số tương ứng.
![]() Bài 10: Anh chị hãy viết các hàm sau:
Bài 10: Anh chị hãy viết các hàm sau:

void ComputeCircle(float&s, float&c, float r = 1.0);

void ComputeRectangle(float&s, float&p, float h = 1.0, float w = 1.0);

void ComputeTriangle(float&s, float&p, float a = 1.0, float b = 1.0, float c = 1.0);

void ComputeSphere(float&v, float&s, float r = 1.0);

void ComputeCylinder(float&v, float&s, float r = 1.0 , float h = 1.0);
![]() Bài 11: Anh (chị) hãy viết thêm hai toán tử nhân và chia hai số phức ở ví dụ 2.18 của chương 2.
Bài 11: Anh (chị) hãy viết thêm hai toán tử nhân và chia hai số phức ở ví dụ 2.18 của chương 2.
![]() Bài 12: Một cấu trúc Date chứa ngày, tháng và năm như sau:
Bài 12: Một cấu trúc Date chứa ngày, tháng và năm như sau:
struct Date
{
int Day; //Có giá trị từ 1 31
int Month; //Có giá trị từ 1 12
int Year; //Biểu diễn bằng 4 chữ số.
};
Anh (chị) hãy viết các hàm định nghĩa các toán tử : + ->>=<<= == != trên cấu trúc Date này.
![]() Bài 13: Một cấu trúc Point3D biểu diễn tọa độ của một điểm trong không gian ba chiều như sau:
Bài 13: Một cấu trúc Point3D biểu diễn tọa độ của một điểm trong không gian ba chiều như sau:
struct Point3D
{
float X;
float Y;
float Z;
};
Anh (chị) hãy viết các hàm định nghĩa các toán tử : + - == != trên cấu trúc Point3D này.
![]() Bài 14: Một cấu trúc Fraction dùng để chứa một phân số như sau:
Bài 14: Một cấu trúc Fraction dùng để chứa một phân số như sau:
struct Fraction
{
int Numerator; //Tử số
int Denominator; //Mẫu số
};
Anh (chị) hãy viết các hàm định nghĩa các toán tử :
+ - * />>=<<= == !=
trên cấu trúc Fraction này.
![]()

Notification Switch
Would you like to follow the 'Lập trình hướng đối tượng' conversation and receive update notifications?