5.6 Inverse trigonometric functions  (Page 4/15)

Evaluating compositions of the form f ( f ⁻¹ ( y )) and f ⁻¹ ( f ( x ))

For any trigonometric function, $f\left(f^{-1}\left(y\right)\right)=y$ for all $y$ in the proper domain for the given function. This follows from the definition of the inverse and from the fact that the range of $f$ was defined to be identical to the domain of $f^{-1}.$ However, we have to be a little more careful with expressions of the form $f^{-1}\left(f\left(x\right)\right).$

Evaluating compositions of the form f ⁻¹ ( g ( x ))

Now that we can compose a trigonometric function with its inverse, we can explore how to evaluate a composition of a trigonometric function and the inverse of another trigonometric function. We will begin with compositions of the form $f^{-1}\left(g\left(x\right)\right).$ For special values of $x,$ we can exactly evaluate the inner function and then the outer, inverse function. However, we can find a more general approach by considering the relation between the two acute angles of a right triangle where one is $\theta ,$ making the other $\frac{\pi }{2}-\theta .$ Consider the sine and cosine of each angle of the right triangle in [link] .

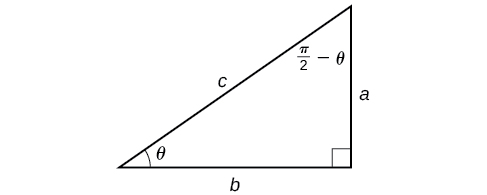
Because $\cos \theta =\frac{b}{c}=\sin \left(\frac{\pi }{2}-\theta \right),$ we have ${\sin }^{-1}\left(\cos \theta \right)=\frac{\pi }{2}-\theta$ if $0\le \theta \le \pi .$ If $\theta$ is not in this domain, then we need to find another angle that has the same cosine as $\theta$ and does belong to the restricted domain; we then subtract this angle from $\frac{\pi }{2}.$ Similarly, $\sin \theta =\frac{a}{c}=\cos \left(\frac{\pi }{2}-\theta \right),$ so ${\cos }^{-1}\left(\sin \theta \right)=\frac{\pi }{2}-\theta$ if $-\frac{\pi }{2}\le \theta \le \frac{\pi }{2}.$ These are just the function-cofunction relationships presented in another way.