8.3 Inverse trigonometric functions  (Page 3/15)

Using a calculator to evaluate inverse trigonometric functions

To evaluate inverse trigonometric functions that do not involve the special angles discussed previously, we will need to use a calculator or other type of technology. Most scientific calculators and calculator-emulating applications have specific keys or buttons for the inverse sine, cosine, and tangent functions. These may be labeled, for example, SIN-1, ARCSIN, or ASIN.

In the previous chapter, we worked with trigonometry on a right triangle to solve for the sides of a triangle given one side and an additional angle. Using the inverse trigonometric functions, we can solve for the angles of a right triangle given two sides, and we can use a calculator to find the values to several decimal places.

In these examples and exercises, the answers will be interpreted as angles and we will use $\theta$ as the independent variable. The value displayed on the calculator may be in degrees or radians, so be sure to set the mode appropriate to the application.

How To

Given two sides of a right triangle like the one shown in [link] , find an angle.

1. If one given side is the hypotenuse of length $h$ and the side of length $a$ adjacent to the desired angle is given, use the equation $\theta ={\cos }^{-1}\left(\frac{a}{h}\right).$
2. If one given side is the hypotenuse of length $h$ and the side of length $p$ opposite to the desired angle is given, use the equation $\theta ={\sin }^{-1}\left(\frac{p}{h}\right).$
3. If the two legs (the sides adjacent to the right angle) are given, then use the equation $\theta ={\tan }^{-1}\left(\frac{p}{a}\right).$

Applying the inverse cosine to a right triangle

Solve the triangle in [link] for the angle $\theta .$

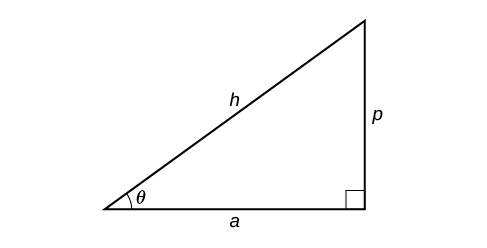
Because we know the hypotenuse and the side adjacent to the angle, it makes sense for us to use the cosine function.

$$\begin{array}{ll}\cos \theta =\frac{9}{12}\hfill & \begin{array}{ccc}& & \end{array}\hfill \\ \theta ={\cos }^{-1}(\frac{9}{12})\hfill & \begin{array}{ccc}& & \end{array}\text{Apply definition of the inverse}.\hfill \\ \theta \approx 0.7227\text{ or about }\mathrm{41.4096°}\hfill & \begin{array}{ccc}& & \end{array}\text{Evaluate}.\hfill \end{array}$$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Try It

Solve the triangle in [link] for the angle $\theta .$

${\sin }^{\mathrm{-1}}(0.6)=\mathrm{36.87°}=0.6435$ radians

Got questions? Get instant answers now!

Finding exact values of composite functions with inverse trigonometric functions

There are times when we need to compose a trigonometric function with an inverse trigonometric function. In these cases, we can usually find exact values for the resulting expressions without resorting to a calculator. Even when the input to the composite function is a variable or an expression, we can often find an expression for the output. To help sort out different cases, let $f(x)$ and $g(x)$ be two different trigonometric functions belonging to the set $\left\{\sin (x),\cos (x),\tan (x)\right\}$ and let $f^{-1}(y)$ and $g^{-1}(y)$ be their inverses.