| << Chapter < Page | Chapter >> Page > |
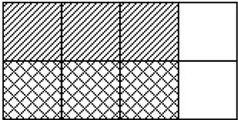
Thus:
(ii) One third ( )of a half ( )looks like this:

Thus
b) Make your own similar sketches for:
(i)
(ii)
c) IMPORTANT!
When multiplying a fraction by a fraction, e.g.
1. We first multiply the numerators together: 2 × 3 = 6
2. Then we multiply the denominators together: 3 × 8 = 24
3. We also simplify where possible:
d) Do you still remember?
To simplify you must always divide the numerator and denominator by the same number.
e) Did you know?
We can make use of cancelling to determine the product.
This entails dividing the numerator and denominator by a common factor.
| e.g. |
| 25 | × | 40 |
| 30 | × | 48 |
| 1 5 × 5 |
| 1 5 × 6 |
| 5 × 8 1 |
| 6 × 8 1 |
| 25 |
| 36 |
A shorter way looks like this:
| 25 | |
| 3 | 30 |
| 40 | 4 1 |
| 48 | 12 |
| 25 |
| 3 × 12 |
| 25 |
| 36 |
We can make use of cross-over and vertical cancelling.
f) Calculate the following by making use of cancelling:
(i)
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
(ii)
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
18.3 Multipilication of mixed numbers
a) TAKE NOTE!
We must first convert the mixed number to an improper fraction and then multiply.
e.g.
Remember: Always simplify your answer!
b) Calculate the following and simplify where possible:
(i)
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
(ii)
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
(iii)
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
19.1 Can you also calculate the answers of the following?
a)
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
b)
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
c)
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
d)
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
19.2 What do you notice when you compare the answers of 19.1?
________________________________________________________________
________________________________________________________________
19.3 Did you know?
If the product of two fractions is 1, then one fraction is the RECIPROCAL of the other. Thus, to get the reciprocal of a fraction, we just swop the numerator and the denominator around!
19.4 Determine the reciprocal of each of the following:
a) = ___________________________________________________
b) 40 = ___________________________________________________
c) = ___________________________________________________
d) = ___________________________________________________
19.5 Explain to a friend how you got c and d’s answers. First write your answers down here.
________________________________________________________________
________________________________________________________________
20. BRAIN-TEASER!
Jodi is metre tall. Sandy is half her length. Grace is of Sandy’s length.
a) How tall is Sandy?
___________________________________________________
___________________________________________________
b) How tall is Grace?
___________________________________________________
___________________________________________________
21. Time for self-assessment
|
YES | NO |
| I can add fractions correctly | ||
| I can find the lowest common multiple of two denominators. | ||
| I can subtract fractions correctly | ||
| I can multiply fractions with natural numbers | ||
| I can multiply fractions with fractions | ||
| I can multiply fractions with mixed numbers | ||
| I know how to use cancelling when I multiply | ||
| I know how to simplify | ||
| I can determine the reciprocal of a fraction |
22. Let us see how quickly you can think! See if you can complete the following mental test in 2 minutes:
| a) 17 + 15 = ............ | i) of 70 = ............ |
| b) 27 + ............ = 42 | j) of 1 minute is ............ seconds |
| c) 52 – 27 = ............ | k) of a day = ............ hours |
| d) 72 – 47 = ............ | l) 56 ÷ 7 = ............ |
| e) 82 – 37 = ............ | m) 72 ÷ 9 = ............ |
| f) 10 × = ............ | n) 48 ÷ 6 = ............ |
| g) of 32 = ............ | o) 10 4 ÷ 10 2 = ............ |
| h) of 56 = ............ |
(15)

Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.7: We know this when the learner estimates and calculates by selecting and using operations appropriate to solving problems that involve:
1.7.3: addition, subtraction and multiplication of common fractions.
Learning Outcome 2: The learner will be able to recognise, describe and represent patterns and relationships, as well as to solve problems using algebraic language and skills.
Assessment Standard 2.1: We know this when the learner investigates and extends numeric and geometric patterns looking for a relationship or rules, including patterns:
2.1.5: represented in tables.

Notification Switch
Would you like to follow the 'Mathematics grade 7' conversation and receive update notifications?