| << Chapter < Page | Chapter >> Page > |
Sometimes the coefficient can be factored from all three terms of the trinomial. This will be our strategy in the next example.
Solve by completing the square.
To complete the square, we need the coefficient of to be one. If we factor out the coefficient of as a common factor, we can continue with solving the equation by completing the square.
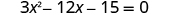 | |
| Factor out the greatest common factor. |
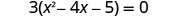 |
| Divide both sides by 3 to isolate the trinomial. |
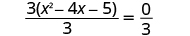 |
| Simplify. |
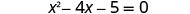 |
| Subtract 5 to get the constant terms on the right. |
 |
| Take half of 4 and square it. |
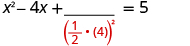 |
| Add 4 to both sides. |
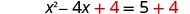 |
| Factor the perfect square trinomial as a binomial square. |
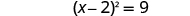 |
| Use the Square Root Property. |
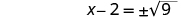 |
| Solve for x. |
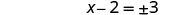 |
| Rewrite to show 2 solutions. |
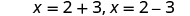 |
| Simplify. |
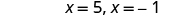 |
Check.
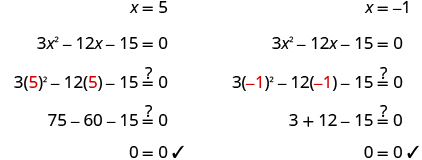 |
To complete the square, the leading coefficient must be one. When the leading coefficient is not a factor of all the terms, we will divide both sides of the equation by the leading coefficient. This will give us a fraction for the second coefficient. We have already seen how to complete the square with fractions in this section.
Solve by completing the square.
Again, our first step will be to make the coefficient of be one. By dividing both sides of the equation by the coefficient of , we can then continue with solving the equation by completing the square.
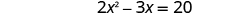 | |
| Divide both sides by 2 to get the coefficient of to be 1. |
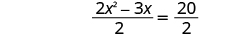 |
| Simplify. |
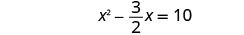 |
| Take half of and square it. |
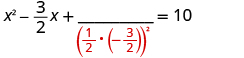 |
| Add to both sides. |
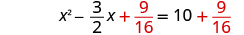 |
| Factor the perfect square trinomial as a binomial square. |
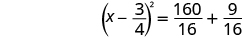 |
| Add the fractions on the right side. |
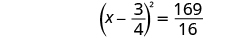 |
| Use the Square Root Property. |
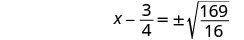 |
| Simplify the radical. |
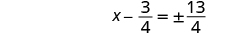 |
| Solve for x. |
 |
| Rewrite to show 2 solutions. |
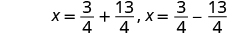 |
| Simplify. |
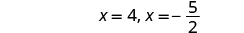 |
| Check. We leave the check for you. |
Solve by completing the square.
Again, our first step will be to make the coefficient of be one. By dividing both sides of the equation by the coefficient of , we can then continue with solving the equation by completing the square.
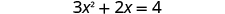 | |
| Divide both sides by 3 to make the coefficient of equal 1. |
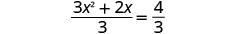 |
| Simplify. |
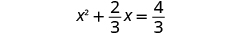 |
| Take half of and square it. |
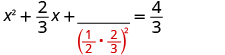 |
| Add to both sides. |
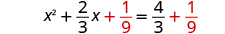 |
| Factor the perfect square trinomial as a binomial square. |
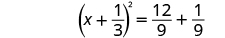 |
| Use the Square Root Property. |
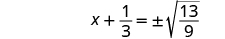 |
| Simplify the radical. |
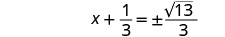 |
| Solve for x . |
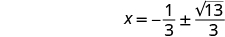 |
| Rewrite to show 2 solutions. |
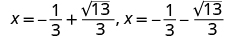 |
| Check. We leave the check for you. |
Access these online resources for additional instruction and practice with solving quadratic equations by completing the square:
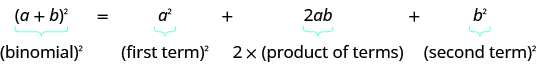
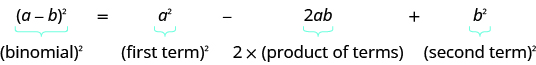
Complete the Square of a Binomial Expression
In the following exercises, complete the square to make a perfect square trinomial. Then, write the result as a binomial squared.
Solve Quadratic Equations of the Form by Completing the Square
In the following exercises, solve by completing the square.
Solve Quadratic Equations of the Form by Completing the Square
In the following exercises, solve by completing the square.
Rafi is designing a rectangular playground to have an area of 320 square feet. He wants one side of the playground to be four feet longer than the other side. Solve the equation for , the length of one side of the playground. What is the length of the other side?
16 feet, 20 feet
Yvette wants to put a square swimming pool in the corner of her backyard. She will have a 3 foot deck on the south side of the pool and a 9 foot deck on the west side of the pool. She has a total area of 1080 square feet for the pool and two decks. Solve the equation for , the length of a side of the pool.
Solve the equation ⓐ by using the Square Root Property and ⓑ by completing the square. ⓒ Which method do you prefer? Why?
ⓐ ⓑ ⓒ Answers will vary.
Solve the equation by completing the square and explain all your steps.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
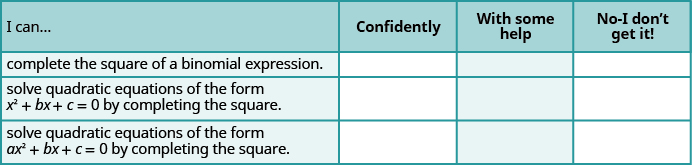
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?