10.2 Solve quadratic equations by completing the square  (Page 3/5)

Solve $x^2+4x=\mathrm{-21}$ by completing the square.

Solution

The variable terms are on the left side.
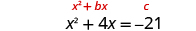Take half of $4$ and square it. $\left(\frac{1}{2}\right(4){)}^2=4$
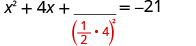Add 4 to both sides.
Factor the perfect square trinomial as a binomial square.
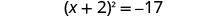Use the Square Root Property.
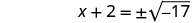We cannot take the square root of a negative number.	There is no real solution.

Got questions? Get instant answers now!

Got questions? Get instant answers now!

In the previous example, there was no real solution because ${\left(x+k\right)}^2$ was equal to a negative number.

Solve $p^2-18p=\mathrm{-6}$ by completing the square.

Solution

The variable terms are on the left side.
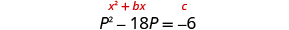Take half of $\text{−}18$ and square it. $\left(\frac{1}{2}\right(\text{−}18){)}^2=81$
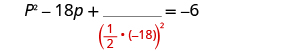Add 81 to both sides.
Factor the perfect square trinomial as a binomial square.
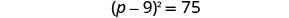Use the Square Root Property.
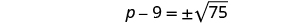Simplify the radical.
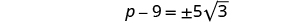Solve for p.
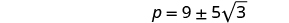Rewrite to show two solutions.
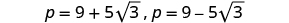Check.

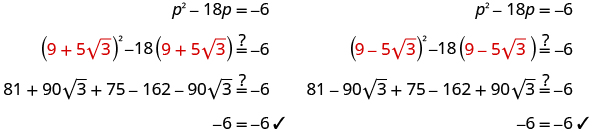Another way to check this would be to use a calculator. Evaluate $p^2-18p$ for both of the solutions. The answer should be $\mathrm{-6}$ .

Got questions? Get instant answers now!

Got questions? Get instant answers now!

We will start the next example by isolating the variable terms on the left side of the equation.

Solve $x^2+10x+4=15$ by completing the square.

Solution

The variable terms are on the left side.
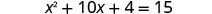Subtract $4$ to get the constant terms on the right side.
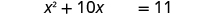Take half of 10 and square it. $\left(\frac{1}{2}\right(10){)}^2=25$
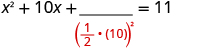Add 25 to both sides.
Factor the perfect square trinomial as a binomial square.
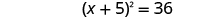Use the Square Root Property.
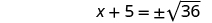Simplify the radical.
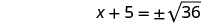Solve for x.
Rewrite to show two equations.
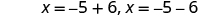Solve the equations.
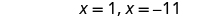Check.

Got questions? Get instant answers now!

Got questions? Get instant answers now!

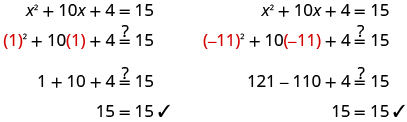To solve the next equation, we must first collect all the variable terms to the left side of the equation. Then, we proceed as we did in the previous examples.

Solve $n^2=3n+11$ by completing the square.

Solution

Subtract 3 n to get the variable terms on the left side.
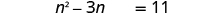Take half of $\text{−}3$ and square it. $\left(\frac{1}{2}\right(\text{−}3){)}^2=\frac{9}{4}$
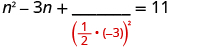Add $\frac{9}{4}$ to both sides.
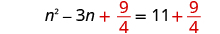Factor the perfect square trinomial as a binomial square.
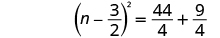Add the fractions on the right side.
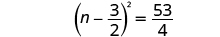Use the Square Root Property.
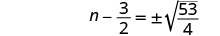Simplify the radical.
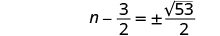Solve for n.
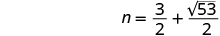Rewrite to show two equations.
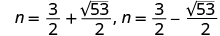Check. We leave the check for you!

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Notice that the left side of the next equation is in factored form. But the right side is not zero, so we cannot use the Zero Product Property. Instead, we multiply the factors and then put the equation into the standard form to solve by completing the square.

Solve $\left(x-3\right)\left(x+5\right)=9$ by completing the square.

Solution

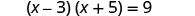We multiply binomials on the left.
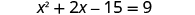Add 15 to get the variable terms on the left side.
Take half of 2 and square it. $\left(\frac{1}{2}\right(2){)}^2=1$
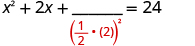Add 1 to both sides.
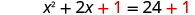Factor the perfect square trinomial as a binomial square.
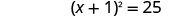Use the Square Root Property.
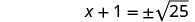Solve for x .
Rewite to show two solutions.
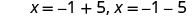Simplify.
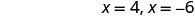Check. We leave the check for you!

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Solve quadratic equations of the form ax ² + bx + c = 0 by completing the square

The process of completing the square works best when the leading coefficient is one, so the left side of the equation is of the form $x^2+bx+c$ . If the $x^2$ term has a coefficient, we take some preliminary steps to make the coefficient equal to one.