| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz. If you miss a problem, go back to the section listed and review the material.
So far, we have solved quadratic equations by factoring and using the Square Root Property. In this section, we will solve quadratic equations by a process called ‘completing the square.’
In the last section, we were able to use the Square Root Property to solve the equation because the left side was a perfect square.
We also solved an equation in which the left side was a perfect square trinomial, but we had to rewrite it the form in order to use the square root property.
What happens if the variable is not part of a perfect square? Can we use algebra to make a perfect square?
Let’s study the binomial square pattern we have used many times. We will look at two examples.
If are real numbers,
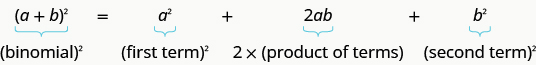
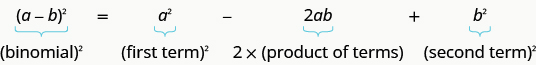
We can use this pattern to “make” a perfect square.
We will start with the expression . Since there is a plus sign between the two terms, we will use the pattern.
Notice that the first term of is a square, .
We now know .
What number can we add to to make a perfect square trinomial?
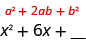
The middle term of the Binomial Squares Pattern, , is twice the product of the two terms of the binomial. This means twice the product of and some number is . So, two times some number must be six. The number we need is The second term in the binomial, must be 3.
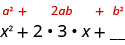
We now know .
Now, we just square the second term of the binomial to get the last term of the perfect square trinomial, so we square three to get the last term, nine.
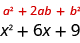
We can now factor to
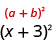
So, we found that adding nine to ‘completes the square,’ and we write it as .
To complete the square of :
Complete the square to make a perfect square trinomial. Then, write the result as a binomial square.
| The coefficient of x is 14. |
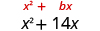 |
| Add 49 to the binomial to complete the square. | |
| Rewrite as a binomial square. |
Complete the square to make a perfect square trinomial. Write the result as a binomial square.
Complete the square to make a perfect square trinomial. Write the result as a binomial square.
Complete the square to make a perfect square trinomial. Then, write the result as a binomial squared.
| The coefficient of m is −26. |
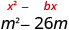 |
| Add 169 to the binomial to complete the square. | |
| Rewrite as a binomial square. |

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?