9.2 Sum and difference identities  (Page 4/6)

Using sum and difference formulas for cofunctions

Now that we can find the sine, cosine, and tangent functions for the sums and differences of angles, we can use them to do the same for their cofunctions. You may recall from Right Triangle Trigonometry that, if the sum of two positive angles is $\frac{\pi }{2},$ those two angles are complements, and the sum of the two acute angles in a right triangle is $\frac{\pi }{2},$ so they are also complements. In [link] , notice that if one of the acute angles is labeled as $\theta ,$ then the other acute angle must be labeled $\left(\frac{\pi }{2}-\theta \right).$

Notice also that $\sin \theta =\cos \left(\frac{\pi }{2}-\theta \right),$ which is opposite over hypotenuse. Thus, when two angles are complimentary, we can say that the sine of $\theta$ equals the cofunction of the complement of $\theta .$ Similarly, tangent and cotangent are cofunctions, and secant and cosecant are cofunctions.

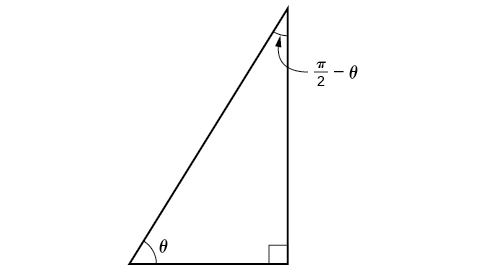
From these relationships, the cofunction identities are formed. Recall that you first encountered these identities in The Unit Circle: Sine and Cosine Functions .

Notice that the formulas in the table may also justified algebraically using the sum and difference formulas. For example, using

we can write

Using the sum and difference formulas to verify identities

Verifying an identity means demonstrating that the equation holds for all values of the variable. It helps to be very familiar with the identities or to have a list of them accessible while working the problems. Reviewing the general rules presented earlier may help simplify the process of verifying an identity.