| << Chapter < Page | Chapter >> Page > |
Let and denote two non-vertical intersecting lines, and let denote the acute angle between and See [link] . Show that
where and are the slopes of and respectively. ( Hint: Use the fact that and )
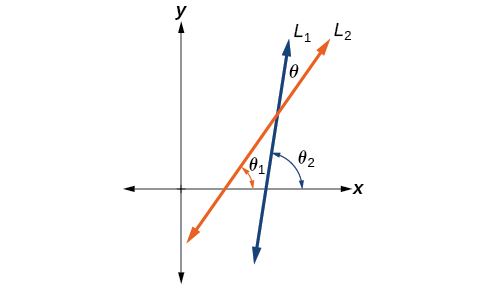
Using the difference formula for tangent, this problem does not seem as daunting as it might.
For a climbing wall, a guy-wire is attached 47 feet high on a vertical pole. Added support is provided by another guy-wire attached 40 feet above ground on the same pole. If the wires are attached to the ground 50 feet from the pole, find the angle between the wires. See [link] .
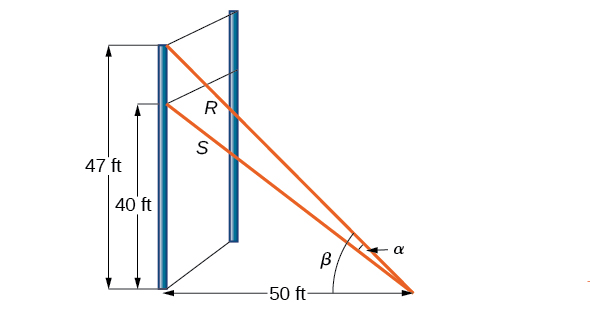
Let’s first summarize the information we can gather from the diagram. As only the sides adjacent to the right angle are known, we can use the tangent function. Notice that and We can then use difference formula for tangent.
Now, substituting the values we know into the formula, we have
Use the distributive property, and then simplify the functions.
Now we can calculate the angle in degrees.
Access these online resources for additional instruction and practice with sum and difference identities.
| Sum Formula for Cosine | |
| Difference Formula for Cosine | |
| Sum Formula for Sine | |
| Difference Formula for Sine | |
| Sum Formula for Tangent | |
| Difference Formula for Tangent | |
| Cofunction identities |

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?