7.2 Right triangle trigonometry

Mt. Everest, which straddles the border between China and Nepal, is the tallest mountain in the world. Measuring its height is no easy task and, in fact, the actual measurement has been a source of controversy for hundreds of years. The measurement process involves the use of triangles and a branch of mathematics known as trigonometry. In this section, we will define a new group of functions known as trigonometric functions, and find out how they can be used to measure heights, such as those of the tallest mountains.

Using right triangles to evaluate trigonometric functions

[link] shows a right triangle with a vertical side of length $y$ and a horizontal side has length $x.$ Notice that the triangle is inscribed in a circle of radius 1. Such a circle, with a center at the origin and a radius of 1, is known as a unit circle    .

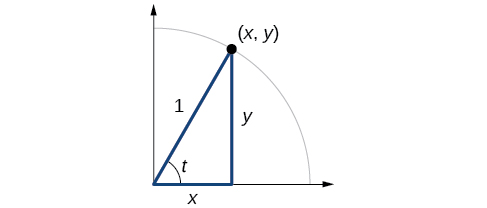
We can define the trigonometric functions in terms an angle t and the lengths of the sides of the triangle. The adjacent side    is the side closest to the angle, x . (Adjacent means “next to.”) The opposite side    is the side across from the angle, y . The hypotenuse    is the side of the triangle opposite the right angle, 1. These sides are labeled in [link] .

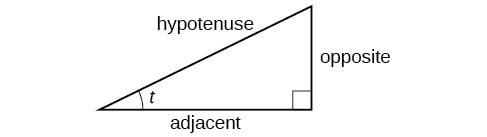
Given a right triangle with an acute angle of $t,$ the first three trigonometric functions are listed.

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “ S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, T angent is o pposite over a djacent.”

For the triangle shown in [link] , we have the following.

Evaluating a trigonometric function of a right triangle

Given the triangle shown in [link] , find the value of $\cos \alpha .$

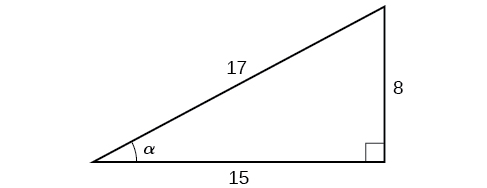
The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17.

$$\begin{array}{ccc}\hfill \cos (\alpha )& =& \frac{\text{adjacent}}{\text{hypotenuse}}\hfill \\ & =& \frac{15}{17}\hfill \end{array}$$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Try It

Given the triangle shown in [link] , find the value of $\text{sin}t.$

$\frac{7}{25}$

Got questions? Get instant answers now!

Reciprocal functions

In addition to sine, cosine, and tangent, there are three more functions. These too are defined in terms of the sides of the triangle.

Take another look at these definitions. These functions are the reciprocals of the first three functions.