| << Chapter < Page | Chapter >> Page > |
The photoelectric effect was explained in 1905 by A. Einstein . Einstein reasoned that if Planck’s hypothesis about energy quanta was correct for describing the energy exchange between electromagnetic radiation and cavity walls, it should also work to describe energy absorption from electromagnetic radiation by the surface of a photoelectrode. He postulated that an electromagnetic wave carries its energy in discrete packets. Einstein’s postulate goes beyond Planck’s hypothesis because it states that the light itself consists of energy quanta. In other words, it states that electromagnetic waves are quantized.
In Einstein’s approach, a beam of monochromatic light of frequency f is made of photons. A photon is a particle of light. Each photon moves at the speed of light and carries an energy quantum A photon’s energy depends only on its frequency f . Explicitly, the energy of a photon is
where is Planck’s constant. In the photoelectric effect, photons arrive at the metal surface and each photon gives away all of its energy to only one electron on the metal surface. This transfer of energy from photon to electron is of the “all or nothing” type, and there are no fractional transfers in which a photon would lose only part of its energy and survive. The essence of a quantum phenomenon is either a photon transfers its entire energy and ceases to exist or there is no transfer at all. This is in contrast with the classical picture, where fractional energy transfers are permitted. Having this quantum understanding, the energy balance for an electron on the surface that receives the energy from a photon is
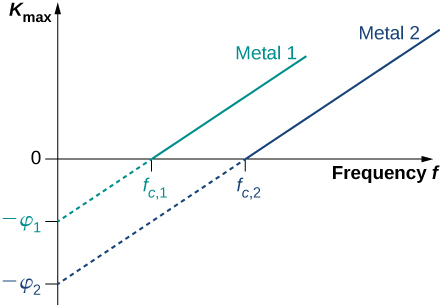
where is the kinetic energy, given by [link] , that an electron has at the very instant it gets detached from the surface. In this energy balance equation, is the energy needed to detach a photoelectron from the surface. This energy is called the work function of the metal. Each metal has its characteristic work function, as illustrated in [link] . To obtain the kinetic energy of photoelectrons at the surface, we simply invert the energy balance equation and use [link] to express the energy of the absorbed photon. This gives us the expression for the kinetic energy of photoelectrons, which explicitly depends on the frequency of incident radiation:
This equation has a simple mathematical form but its physics is profound. We can now elaborate on the physical meaning behind [link] .
| Typical Values of the Work Function for Some Common Metals | |
|---|---|
| Metal | (eV) |
| Na | 2.46 |
| Al | 4.08 |
| Pb | 4.14 |
| Zn | 4.31 |
| Fe | 4.50 |
| Cu | 4.70 |
| Ag | 4.73 |
| Pt | 6.35 |
In Einstein’s interpretation, interactions take place between individual electrons and individual photons. The absence of a lag time means that these one-on-one interactions occur instantaneously. This interaction time cannot be increased by lowering the light intensity. The light intensity corresponds to the number of photons arriving at the metal surface per unit time. Even at very low light intensities, the photoelectric effect still occurs because the interaction is between one electron and one photon. As long as there is at least one photon with enough energy to transfer it to a bound electron, a photoelectron will appear on the surface of the photoelectrode.

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?