6.2 Photoelectric effect  (Page 2/17)

The intensity of incident radiation and the kinetic energy of photoelectrons

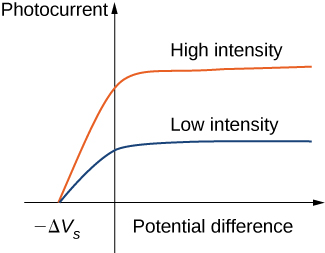
Typical experimental curves are shown in [link] , in which the photocurrent is plotted versus the applied potential difference between the electrodes. For the positive potential difference, the current steadily grows until it reaches a plateau. Furthering the potential increase beyond this point does not increase the photocurrent at all. A higher intensity of radiation produces a higher value of photocurrent. For the negative potential difference, as the absolute value of the potential difference increases, the value of the photocurrent decreases and becomes zero at the stopping potential. For any intensity of incident radiation, whether the intensity is high or low, the value of the stopping potential always stays at one value.

To understand why this result is unusual from the point of view of classical physics, we first have to analyze the energy of photoelectrons. A photoelectron that leaves the surface has kinetic energy K . It gained this energy from the incident electromagnetic wave. In the space between the electrodes, a photoelectron moves in the electric potential and its energy changes by the amount $q\text{Δ}V,$ where $\text{Δ}V$ is the potential difference and $q=\text{−}e.$ Because no forces are present but electric force, by applying the work-energy theorem, we obtain the energy balance $\text{Δ}K-e\text{Δ}V=0$ for the photoelectron, where $\text{Δ}K$ is the change in the photoelectron’s kinetic energy. When the stopping potential $\text{−}\text{Δ}{V}_s$ is applied, the photoelectron loses its initial kinetic energy $K_i$ and comes to rest. Thus, its energy balance becomes $(0-K_i)-e(\text{−}\text{Δ}{V}_s)=0,$ so that $K_i=e\text{Δ}{V}_s.$ In the presence of the stopping potential, the largest kinetic energy $K_{\text{max}}$ that a photoelectron can have is its initial kinetic energy, which it has at the surface of the photoelectrode. Therefore, the largest kinetic energy of photoelectrons can be directly measured by measuring the stopping potential:

At this point we can see where the classical theory is at odds with the experimental results. In classical theory, the photoelectron absorbs electromagnetic energy in a continuous way; this means that when the incident radiation has a high intensity, the kinetic energy in [link] is expected to be high. Similarly, when the radiation has a low intensity, the kinetic energy is expected to be low. But the experiment shows that the maximum kinetic energy of photoelectrons is independent of the light intensity.

The presence of a cut-off frequency

For any metal surface, there is a minimum frequency of incident radiation below which photocurrent does not occur. The value of this cut-off frequency    for the photoelectric effect is a physical property of the metal: Different materials have different values of cut-off frequency. Experimental data show a typical linear trend (see [link] ). The kinetic energy of photoelectrons at the surface grows linearly with the increasing frequency of incident radiation. Measurements for all metal surfaces give linear plots with one slope. None of these observed phenomena is in accord with the classical understanding of nature. According to the classical description, the kinetic energy of photoelectrons should not depend on the frequency of incident radiation at all, and there should be no cut-off frequency. Instead, in the classical picture, electrons receive energy from the incident electromagnetic wave in a continuous way, and the amount of energy they receive depends only on the intensity of the incident light and nothing else. So in the classical understanding, as long as the light is shining, the photoelectric effect is expected to continue.