| << Chapter < Page | Chapter >> Page > |
Consider a point source of light at point P in front of a convex surface made of glass (see [link] ). Let R be the radius of curvature, be the refractive index of the medium in which object point P is located, and be the refractive index of the medium with the spherical surface. We want to know what happens as a result of refraction at this interface.
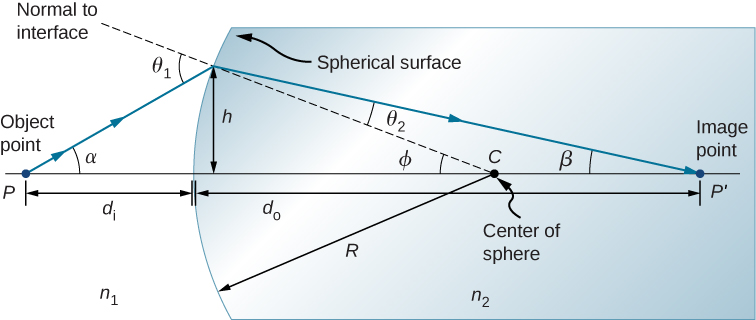
Because of the symmetry involved, it is sufficient to examine rays in only one plane. The figure shows a ray of light that starts at the object point P , refracts at the interface, and goes through the image point . We derive a formula relating the object distance , the image distance , and the radius of curvature R .
Applying Snell’s law to the ray emanating from point P gives . We work in the small-angle approximation, so and Snell’s law then takes the form
From the geometry of the figure, we see that
Inserting these expressions into Snell’s law gives
Using the diagram, we calculate the tangent of the angles :
Again using the small-angle approximation, we find that , so the above relationships become
Putting these angles into Snell’s law gives
We can write this more conveniently as
If the object is placed at a special point called the first focus , or the object focus , then the image is formed at infinity, as shown in part (a) of [link] .
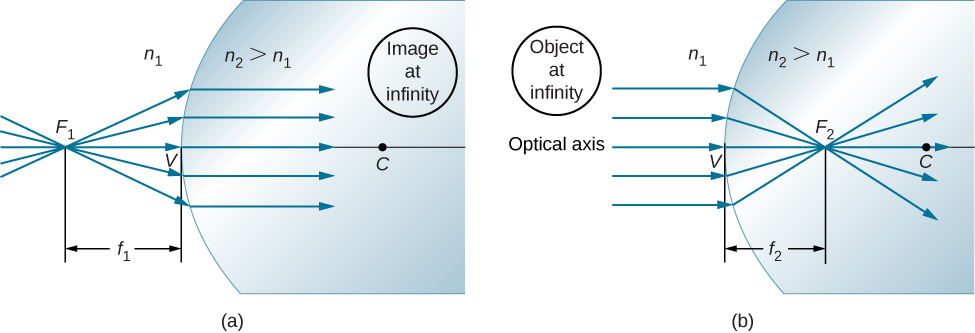
We can find the location of the first focus by setting in the preceding equation.
Similarly, we can define a second focus or image focus where the image is formed for an object that is far away [part (b)]. The location of the second focus is obtained from [link] by setting :
Note that the object focus is at a different distance from the vertex than the image focus because .
Although we derived this equation for refraction at a convex surface, the same expression holds for a concave surface, provided we use the following sign convention:
This section explains how a single refracting interface forms images.
Derive the formula for the apparent depth of a fish in a fish tank using Snell’s law.
Use a ruler and a protractor to find the image by refraction in the following cases. Assume an air-glass interface. Use a refractive index of 1 for air and of 1.5 for glass. ( Hint : Use Snell’s law at the interface.)
(a) A point object located on the axis of a concave interface located at a point within the focal length from the vertex.
(b) A point object located on the axis of a concave interface located at a point farther than the focal length from the vertex.
(c) A point object located on the axis of a convex interface located at a point within the focal length from the vertex.
(d) A point object located on the axis of a convex interface located at a point farther than the focal length from the vertex.
(e) Repeat (a)–(d) for a point object off the axis.
answers may vary
An object is located in air 30 cm from the vertex of a concave surface made of glass with a radius of curvature 10 cm. Where does the image by refraction form and what is its magnification? Use and .
An object is located in air 30 cm from the vertex of a convex surface made of glass with a radius of curvature 80 cm. Where does the image by refraction form and what is its magnification?
An object is located in water 15 cm from the vertex of a concave surface made of glass with a radius of curvature 10 cm. Where does the image by refraction form and what is its magnification? Use and .
An object is located in water 30 cm from the vertex of a convex surface made of Plexiglas with a radius of curvature of 80 cm. Where does the image form by refraction and what is its magnification? and .
An object is located in air 5 cm from the vertex of a concave surface made of glass with a radius of curvature 20 cm. Where does the image form by refraction and what is its magnification? Use and .
Derive the spherical interface equation for refraction at a concave surface. ( Hint : Follow the derivation in the text for the convex surface.)
proof

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?