5.5 The lorentz transformation  (Page 7/12)

Lorentz transformations in space-time

We have already noted how the Lorentz transformation leaves

unchanged and corresponds to a rotation of axes in the four-dimensional space-time. If the S and $\text{S}\prime$ frames are in relative motion along their shared x -direction the space and time axes of $\text{S}\prime$ are rotated by an angle $\alpha$ as seen from S, in the way shown in shown in [link] , where:

This differs from a rotation in the usual three-dimension sense, insofar as the two space-time axes rotate toward each other symmetrically in a scissors-like way, as shown. The rotation of the time and space axes are both through the same angle. The mesh of dashed lines parallel to the two axes show how coordinates of an event would be read along the primed axes. This would be done by following a line parallel to the $x\prime$ and one parallel to the $t\prime$ -axis, as shown by the dashed lines. The length scale of both axes are changed by:

The line labeled $\text{“}v=c\text{”}$ at $45\text{°}$ to the x -axis corresponds to the edge of the light cone, and is unaffected by the Lorentz transformation, in accordance with the second postulate of relativity. The $\text{“}v=c\text{”}$ line, and the light cone it represents, are the same for both the S and $\text{S}\prime$ frame of reference.

Simultaneity

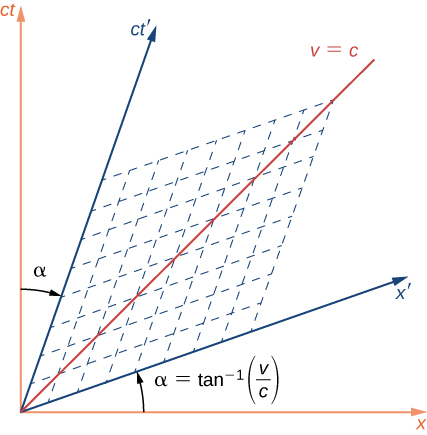
Simultaneity of events at separated locations depends on the frame of reference used to describe them, as given by the scissors-like “rotation” to new time and space coordinates as described. If two events have the same t values in the unprimed frame of reference, they need not have the same values measured along the $ct\prime \text{-axis,}$ and would then not be simultaneous in the primed frame.

As a specific example, consider the near-light-speed train in which flash lamps at the two ends of the car have flashed simultaneously in the frame of reference of an observer on the ground. The space-time graph is shown [link] . The flashes of the two lamps are represented by the dots labeled “Left flash lamp” and “Right flash lamp” that lie on the light cone in the past. The world line of both pulses travel along the edge of the light cone to arrive at the observer on the ground simultaneously. Their arrival is the event at the origin. They therefore had to be emitted simultaneously in the unprimed frame, as represented by the point labeled as t (both). But time is measured along the $ct\prime \text{-axis}$ in the frame of reference of the observer seated in the middle of the train car. So in her frame of reference, the emission event of the bulbs labeled as $t\prime$ (left) and $t\prime$ (right) were not simultaneous.

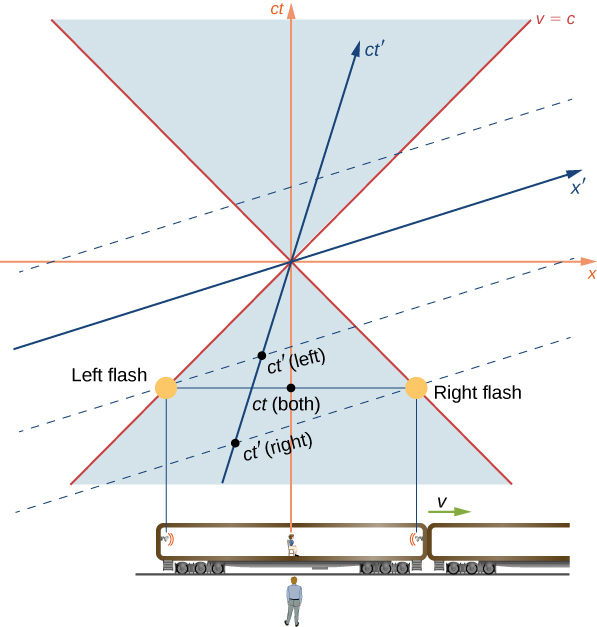
In terms of the space-time diagram, the two observers are merely using different time axes for the same events because they are in different inertial frames, and the conclusions of both observers are equally valid. As the analysis in terms of the space-time diagrams further suggests, the property of how simultaneity of events depends on the frame of reference results from the properties of space and time itself, rather than from anything specifically about electromagnetism.