9.1 Types of molecular bonds  (Page 3/14)

For a sodium ion in an ionic NaCl crystal, the expression for Coulomb potential energy $U_{\text{coul}}$ must be modified by a factor known as the Madelung constant    . This factor takes into account the interaction of the sodium ion with all nearby chloride and sodium ions. The Madelung constant for a NaCl crystal is about 1.75. This value implies an equilibrium separation distance between ${\text{Na}}^{+}\text{and}{\text{Cl}}^{\text{−}}$ ions of 0.280 nm—slightly larger than for diatomic NaCl. We will return to this point again later.

Covalent bonds

In an ionic bond, an electron transfers from one atom to another. However, in a covalent bond, an electron is shared between two atoms. The ionic bonding mechanism cannot explain the existence of such molecules as ${\text{H}}_2\text{,}{\text{O}}_2,$ and CO, since no separation distance exists for which the negative potential energy of attraction is greater in magnitude than the energy needed to create ions. Understanding precisely how such molecules are covalently bonded relies on a deeper understanding of quantum mechanics that goes beyond the coverage of this book, but we will qualitatively describe the mechanisms in the following section.

Covalent bonds can be understood using the simple example of a ${\text{H}}_2^{+}$ molecule, which consists of one electron in the electric field of two protons. This system can be modeled by an electron in a double square well ( [link] ). The electron is equally likely to be found in each well, so the wave function is either symmetric or antisymmetric about a point midway between the wells.

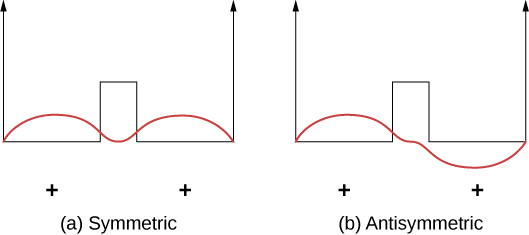
Now imagine that the two wells are separated by a large distance. In the ground state, the wave function exists in one of two possible states: either a single positive peak (a sine wave-like “hump”) in both wells (symmetric case), or a positive peak in one well and a negative peak in the other (antisymmetric case). These states have the same energy. However, when the wells are brought together, the symmetric wave function becomes the ground state and the antisymmetric state becomes the first excited state—in other words, the energy level of the electron is split. Notice, the space-symmetric state becomes the energetically favorable (lower energy) state.

The same analysis is appropriate for an electron bound to two hydrogen atoms. Here, the shapes of the ground-state wave functions have the form $e^{\text{−}r\text{/}{a}_0}$ or $e^{(\text{−}|x|\text{/}{a}_0)}$ in one dimension. The energetically favorable, space-symmetric state implies a high charge density midway between the protons where the electrons are likely to pull the positively charged protons together.

If a second electron is added to this system to form a ${\text{H}}_2$ molecule, the wave function must describe both particles, including their spatial relationship and relative spins. This wave function must also respect the indistinguishability of electrons. (“If you’ve seen one electron, you’ve seen them all.”) In particular, switching or exchanging the electrons should not produce an observable effect, a property called exchange symmetry    . Exchange symmetry can be symmetric , producing no change in the wave function, or antisymmetric , producing an overall change in the sign of the wave function—neither of which is observable.