1.7 Polarization  (Page 38/20)

Polarizing sunglasses are familiar to most of us. They have a special ability to cut the glare of light reflected from water or glass ( [link] ). They have this ability because of a wave characteristic of light called polarization. What is polarization? How is it produced? What are some of its uses? The answers to these questions are related to the wave character of light.

Malus’s law

Light is one type of electromagnetic (EM) wave. As noted in the previous chapter on Electromagnetic Waves , EM waves are transverse waves consisting of varying electric and magnetic fields that oscillate perpendicular to the direction of propagation ( [link] ). However, in general, there are no specific directions for the oscillations of the electric and magnetic fields; they vibrate in any randomly oriented plane perpendicular to the direction of propagation. Polarization is the attribute that a wave’s oscillations do have a definite direction relative to the direction of propagation of the wave. (This is not the same type of polarization as that discussed for the separation of charges.) Waves having such a direction are said to be polarized    . For an EM wave, we define the direction of polarization    to be the direction parallel to the electric field. Thus, we can think of the electric field arrows as showing the direction of polarization, as in [link] .

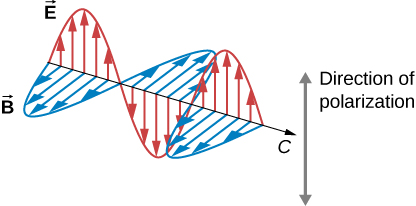
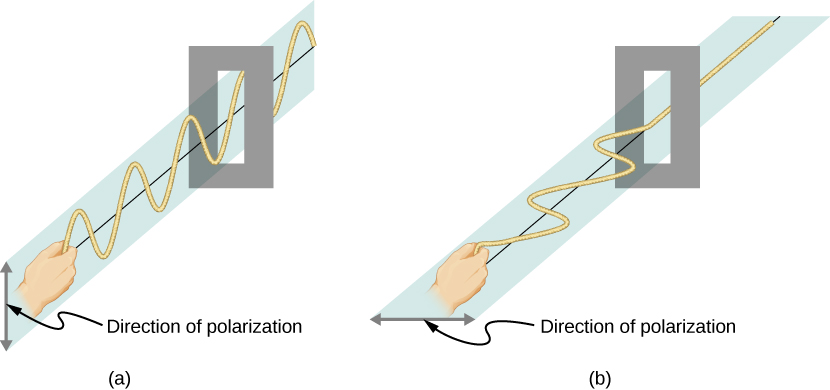
To examine this further, consider the transverse waves in the ropes shown in [link] . The oscillations in one rope are in a vertical plane and are said to be vertically polarized    . Those in the other rope are in a horizontal plane and are horizontally polarized    . If a vertical slit is placed on the first rope, the waves pass through. However, a vertical slit blocks the horizontally polarized waves. For EM waves, the direction of the electric field is analogous to the disturbances on the ropes.