8.2 Capacitors in series and in parallel (Page 3/5)

University physics volume 2 Page 3 / 5

Capacitor networks are usually some combination of series and parallel connections, as shown in [link] . To find the net capacitance of such combinations, we identify parts that contain only series or only parallel connections, and find their equivalent capacitances. We repeat this process until we can determine the equivalent capacitance of the entire network. The following example illustrates this process.

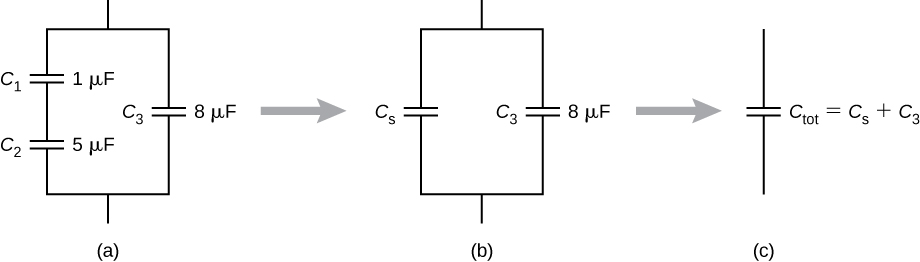
Figure a shows capacitors C1 and C2 in series and C3 in parallel with them. The value of C1 is 1 micro Farad, that of C2 is 5 micro Farad and that of C3 is 8 micro Farad. Figure b is the same as figure a, with C1 and C2 being replaced with equivalent capacitor Cs. Figure c is the same as figure b with Cs and C3 being replaced with equivalent capacitor C tot. C tot is equal to Cs plus C3. — (a) This circuit contains both series and parallel connections of capacitors. (b) $C_{1}$ and $C_{2}$ are in series; their equivalent capacitance is $C_{S} .$ (c) The equivalent capacitance $C_{S}$ is connected in parallel with $C_{3} .$ Thus, the equivalent capacitance of the entire network is the sum of $C_{S}$ and $C_{3} .$

Equivalent capacitance of a network

Find the total capacitance of the combination of capacitors shown in [link] . Assume the capacitances are known to three decimal places

(C_{1} = 1.000 μ F, C_{2} = 5.000 μ F,

C_{3} = 8.000 μ F) .

Round your answer to three decimal places.

Strategy

We first identify which capacitors are in series and which are in parallel. Capacitors

C_{1}

and

C_{2}

are in series. Their combination, labeled

C_{S},

is in parallel with

C_{3} .

Solution

Since

C_{1} and C_{2}

are in series, their equivalent capacitance

C_{S}

is obtained with [link] :

\frac{1}{C_{S}} = \frac{1}{C_{1}} + \frac{1}{C_{2}} = \frac{1}{1.000 μ F} + \frac{1}{5.000 μ F} = \frac{1.200}{μ F} \Rightarrow C_{S} = 0.833 μ F .

Capacitance $C_{S}$ is connected in parallel with the third capacitance $C_{3}$ , so we use [link] to find the equivalent capacitance C of the entire network:

C = C_{S} + C_{3} = 0.833 μ F + 8.000 μ F = 8.833 μ F .

Got questions? Get instant answers now!

Network of capacitors

Determine the net capacitance C of the capacitor combination shown in [link] when the capacitances are

C_{1} = 12.0 μ F, C_{2} = 2.0 μ F,

and

C_{3} = 4.0 μ F

. When a 12.0-V potential difference is maintained across the combination, find the charge and the voltage across each capacitor.

Strategy

We first compute the net capacitance

C_{23}

of the parallel connection

C_{2}

and

C_{3}

. Then C is the net capacitance of the series connection

C_{1}

and

C_{23}

. We use the relation

C = Q / V

to find the charges

Q_{1}

Q_{2}

, and

Q_{3}

, and the voltages

V_{1}

V_{2}

, and

V_{3}

, across capacitors 1, 2, and 3, respectively.

Solution

The equivalent capacitance for

C_{2}

and

C_{3}

C_{23} = C_{2} + C_{3} = 2.0 μ F + 4.0 μ F = 6.0 μ F .

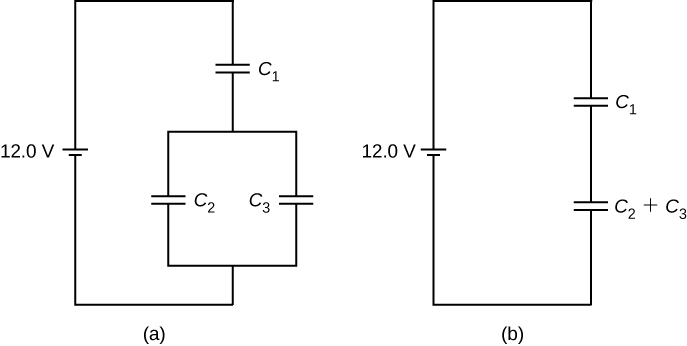
The entire three-capacitor combination is equivalent to two capacitors in series,

\frac{1}{C} = \frac{1}{12.0 μ F} + \frac{1}{6.0 μ F} = \frac{1}{4.0 μ F} \Rightarrow C = 4.0 μ F .

Consider the equivalent two-capacitor combination in [link] (b). Since the capacitors are in series, they have the same charge, $Q_{1} = Q_{23}$ . Also, the capacitors share the 12.0-V potential difference, so

12.0 V = V_{1} + V_{23} = \frac{Q_{1}}{C_{1}} + \frac{Q_{23}}{C_{23}} = \frac{Q_{1}}{12.0 μ F} + \frac{Q_{1}}{6.0 μ F} \Rightarrow Q_{1} = 48.0 μ C .

Now the potential difference across capacitor 1 is

V_{1} = \frac{Q_{1}}{C_{1}} = \frac{48.0 μ C}{12.0 μ F} = 4.0 V .

Because capacitors 2 and 3 are connected in parallel, they are at the same potential difference:

V_{2} = V_{3} = 12.0 V - 4.0 V = 8.0 V .

Hence, the charges on these two capacitors are, respectively,

\begin{array}{l} Q_{2} = C_{2} V_{2} = (2.0 μ F) (8.0 V) = 16.0 μ C, \\ Q_{3} = C_{3} V_{3} = (4.0 μ F) (8.0 V) = 32.0 μ C . \end{array}

Significance

As expected, the net charge on the parallel combination of

C_{2}

and

C_{3}

Q_{23} = Q_{2} + Q_{3} = 48.0 μ C .

Got questions? Get instant answers now!

Check Your Understanding Determine the net capacitance C of each network of capacitors shown below. Assume that $C_{1} = 1.0 pF$ , $C_{2} = 2.0 pF$ , $C_{3} = 4.0 pF$ , and $C_{4} = 5.0 pF$ . Find the charge on each capacitor, assuming there is a potential difference of 12.0 V across each network.

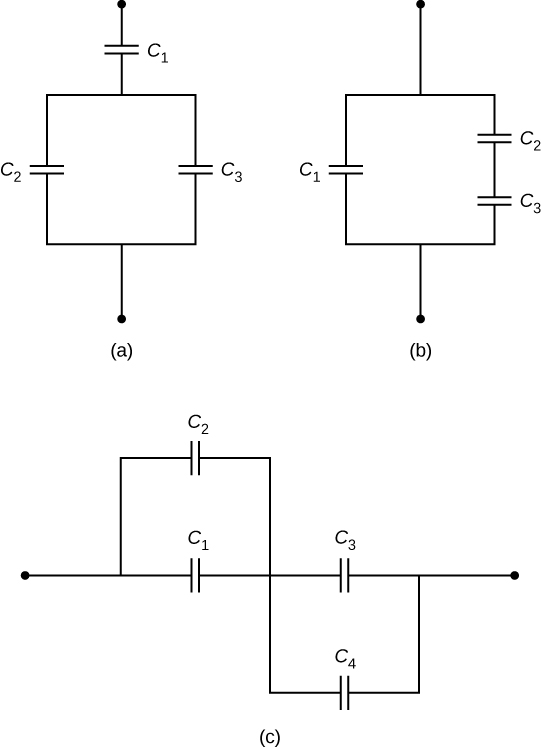
Figure a shows capacitors C2 and C3 in parallel with each other. They are in series with C1. Figure b shows capacitors C2 and C3 in series with each other. They are in parallel with C1. Figure c shows capacitors C1 and C2 in parallel with each other and capacitors C3 and C4 in parallel with each other. These combinations are connected in series.

a. $C = 0.86 pF, Q_{1} = 10 pC, Q_{2} = 3.4 pC, Q_{3} = 6.8 pC$ ;
b. $C = 2.3 pF, Q_{1} = 12 pC, Q_{2} = Q_{3} = 16 pC$ ;
c. $C = 2.3 pF, Q_{1} = 9.0 pC, Q_{2} = 18 pC, Q_{3} = 12 pC, Q_{4} = 15 pC$

Got questions? Get instant answers now!

Summary

When several capacitors are connected in a series combination, the reciprocal of the equivalent capacitance is the sum of the reciprocals of the individual capacitances.
When several capacitors are connected in a parallel combination, the equivalent capacitance is the sum of the individual capacitances.
When a network of capacitors contains a combination of series and parallel connections, we identify the series and parallel networks, and compute their equivalent capacitances step by step until the entire network becomes reduced to one equivalent capacitance.

Conceptual questions

If you wish to store a large amount of charge in a capacitor bank, would you connect capacitors in series or in parallel? Explain.

Got questions? Get instant answers now!

What is the maximum capacitance you can get by connecting three $1.0 - μ F$ capacitors? What is the minimum capacitance?

$3.0 μ F, 0.33 μ F$

Got questions? Get instant answers now!

Problems

A 4.00-pF is connected in series with an 8.00-pF capacitor and a 400-V potential difference is applied across the pair. (a) What is the charge on each capacitor? (b) What is the voltage across each capacitor?

a. 1.07 nC; b. 267 V, 133 V

Got questions? Get instant answers now!

Three capacitors, with capacitances of $C_{1} = 2.0 μ F,$ $C_{2} = 3.0 μ F$ , and $C_{3} = 6.0 μ F,$ respectively, are connected in parallel. A 500-V potential difference is applied across the combination. Determine the voltage across each capacitor and the charge on each capacitor.

Got questions? Get instant answers now!

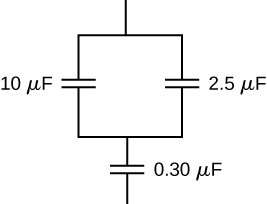
Find the total capacitance of this combination of series and parallel capacitors shown below.

Figure shows capacitors of value 10 micro Farad and 2.5 micro Farad connected in parallel with each other. These are connected in series with a capacitor of value 0.3 micro Farad.

$0.29 μ F$

Got questions? Get instant answers now!

Suppose you need a capacitor bank with a total capacitance of 0.750 F but you have only 1.50-mF capacitors at your disposal. What is the smallest number of capacitors you could connect together to achieve your goal, and how would you connect them?

500 capacitors; connected in parallel

Got questions? Get instant answers now!

What total capacitances can you make by connecting a $5.00 - μ F$ and a $8.00 - μ F$ capacitor?

$3.08 μ F$ (series) and $13.0 μ F$ (parallel)

Got questions? Get instant answers now!

Find the equivalent capacitance of the combination of series and parallel capacitors shown below.

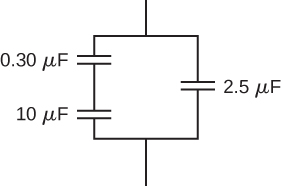
Figure shows capacitors of value 0.3 micro Farad and 10 micro Farad connected in series with each other. These are connected in parallel with a capacitor of value 2.5 micro Farad.

Got questions? Get instant answers now!

Find the net capacitance of the combination of series and parallel capacitors shown below.

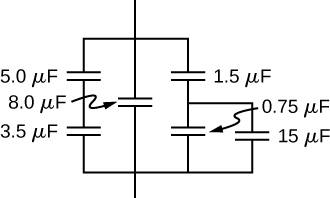
Figure shows a circuit with three branches connected in parallel with each other. Brach 1 has capacitors of value 5 micro Farad and 3.5 micro Farad connected in series with each other. Brach 2 has a capacitor of value 8 micro Farad. Brach 3 has three capacitors. Two of these, having values 0.75 micro Farad and 15 micro Farad are connected in parallel with each other. These are in series with the third capacitor of value 1.5 micro Farad.

$11.4 μ F$

Got questions? Get instant answers now!

A 40-pF capacitor is charged to a potential difference of 500 V. Its terminals are then connected to those of an uncharged 10-pF capacitor. Calculate: (a) the original charge on the 40-pF capacitor; (b) the charge on each capacitor after the connection is made; and (c) the potential difference across the plates of each capacitor after the connection.

Got questions? Get instant answers now!

A $2.0 - μ F$ capacitor and a $4.0 - μ F$ capacitor are connected in series across a 1.0-kV potential. The charged capacitors are then disconnected from the source and connected to each other with terminals of like sign together. Find the charge on each capacitor and the voltage across each capacitor.

0.89 mC; 1.78 mC; 444 V

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, University physics volume 2. OpenStax CNX. Oct 06, 2016 Download for free at http://cnx.org/content/col12074/1.3

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'University physics volume 2' conversation and receive update notifications?

Ask

©flickr: Jonathan	Power By Megan Earhart Start Quiz
	Biology Exam Final By Savannah Parrish Start Exam
	24 AP 24 Metabolism Nutrition MCQ By OpenStax Start Quiz
	Information Technology By Subramanian Divya Start Quiz
	25 AP 25 Urinary System MCQ By OpenStax Start Quiz
	16 AP 16 Neurological Essay Exam By OpenStax Start Flashcards
	3 Neuroscience Exam 2004 4 By David Corey Start Exam
	Nutrition Exam By Hannah Sheth Start Quiz
	6 Psychology MCQ 2010 2 Exam By John Gabrieli Start Exam
	Deciduous Forest By Hope Percle Start Quiz