8.2 Capacitors in series and in parallel  (Page 2/5)

Potential V is measured across an equivalent capacitor that holds charge Q and has an equivalent capacitance $C_{\text{S}}$ . Entering the expressions for $V_1$ , $V_2$ , and $V_3$ , we get

Canceling the charge Q , we obtain an expression containing the equivalent capacitance, $C_{\text{S}}$ , of three capacitors connected in series:

This expression can be generalized to any number of capacitors in a series network.

The parallel combination of capacitors

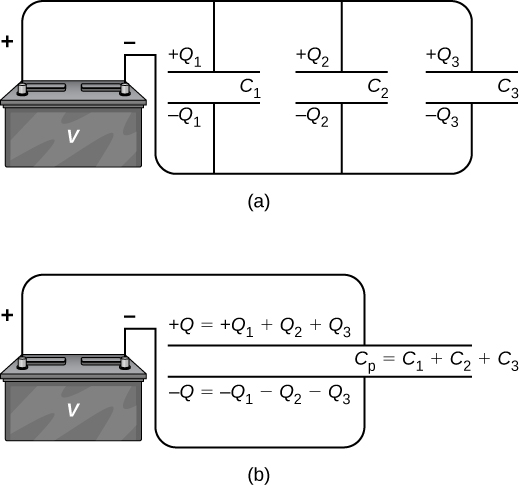
A parallel combination of three capacitors, with one plate of each capacitor connected to one side of the circuit and the other plate connected to the other side, is illustrated in [link] (a). Since the capacitors are connected in parallel, they all have the same voltage V across their plates . However, each capacitor in the parallel network may store a different charge. To find the equivalent capacitance $C_{\text{P}}$ of the parallel network, we note that the total charge Q stored by the network is the sum of all the individual charges:

On the left-hand side of this equation, we use the relation $Q=C_{\text{P}}V$ , which holds for the entire network. On the right-hand side of the equation, we use the relations $Q_1=C_{1}V,Q_2=C_{2}V,$ and $Q_3=C_{3}V$ for the three capacitors in the network. In this way we obtain

This equation, when simplified, is the expression for the equivalent capacitance of the parallel network of three capacitors:

This expression is easily generalized to any number of capacitors connected in parallel in the network.