8.2 Capacitors in series and in parallel  (Page 7/5)

Several capacitors can be connected together to be used in a variety of applications. Multiple connections of capacitors behave as a single equivalent capacitor. The total capacitance of this equivalent single capacitor depends both on the individual capacitors and how they are connected. Capacitors can be arranged in two simple and common types of connections, known as series and parallel , for which we can easily calculate the total capacitance. These two basic combinations, series and parallel, can also be used as part of more complex connections.

The series combination of capacitors

[link] illustrates a series combination of three capacitors, arranged in a row within the circuit. As for any capacitor, the capacitance of the combination is related to the charge and voltage by using [link] . When this series combination is connected to a battery with voltage V , each of the capacitors acquires an identical charge Q . To explain, first note that the charge on the plate connected to the positive terminal of the battery is $+Q$ and the charge on the plate connected to the negative terminal is $\text{−}Q$ . Charges are then induced on the other plates so that the sum of the charges on all plates, and the sum of charges on any pair of capacitor plates, is zero. However, the potential drop $V_1=Q\text{/}{C}_1$ on one capacitor may be different from the potential drop $V_2=Q\text{/}{C}_2$ on another capacitor, because, generally, the capacitors may have different capacitances. The series combination of two or three capacitors resembles a single capacitor with a smaller capacitance. Generally, any number of capacitors connected in series is equivalent to one capacitor whose capacitance (called the equivalent capacitance ) is smaller than the smallest of the capacitances in the series combination. Charge on this equivalent capacitor is the same as the charge on any capacitor in a series combination: That is, all capacitors of a series combination have the same charge . This occurs due to the conservation of charge in the circuit. When a charge Q in a series circuit is removed from a plate of the first capacitor (which we denote as $\text{−}Q$ ), it must be placed on a plate of the second capacitor (which we denote as $+Q),$ and so on.

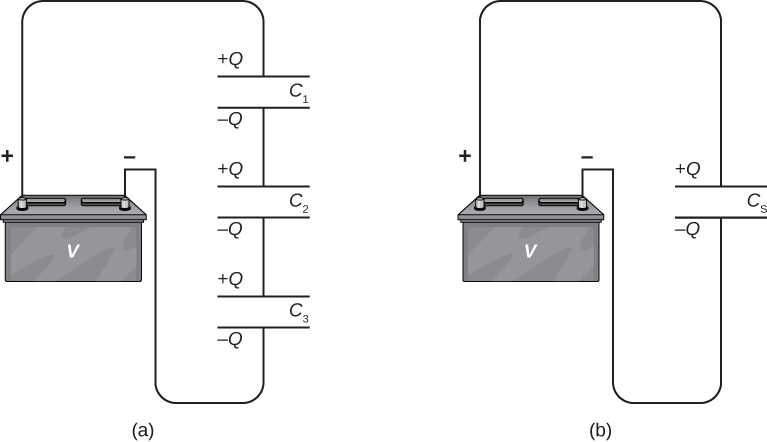
We can find an expression for the total (equivalent) capacitance by considering the voltages across the individual capacitors. The potentials across capacitors 1, 2, and 3 are, respectively, $V_1=Q\text{/}{C}_1$ , $V_2=Q\text{/}{C}_2$ , and $V_3=Q\text{/}{C}_3$ . These potentials must sum up to the voltage of the battery, giving the following potential balance: