| << Chapter < Page | Chapter >> Page > |
From this equation we see that the acceleration vector has magnitude and is directed opposite the position vector, toward the origin, because
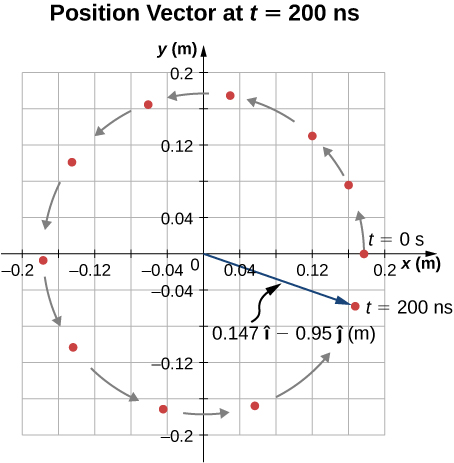
The position of the particle at with A = 0.175 m is
From this result we see that the proton is located slightly below the x -axis. This is shown in [link] .
Circular motion does not have to be at a constant speed. A particle can travel in a circle and speed up or slow down, showing an acceleration in the direction of the motion.
In uniform circular motion, the particle executing circular motion has a constant speed and the circle is at a fixed radius. If the speed of the particle is changing as well, then we introduce an additional acceleration in the direction tangential to the circle. Such accelerations occur at a point on a top that is changing its spin rate, or any accelerating rotor. In Displacement and Velocity Vectors we showed that centripetal acceleration is the time rate of change of the direction of the velocity vector. If the speed of the particle is changing, then it has a tangential acceleration that is the time rate of change of the magnitude of the velocity:
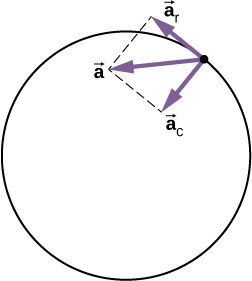
The direction of tangential acceleration is tangent to the circle whereas the direction of centripetal acceleration is radially inward toward the center of the circle. Thus, a particle in circular motion with a tangential acceleration has a total acceleration that is the vector sum of the centripetal and tangential accelerations:
The acceleration vectors are shown in [link] . Note that the two acceleration vectors and are perpendicular to each other, with in the radial direction and in the tangential direction. The total acceleration points at an angle between and

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?