| << Chapter < Page | Chapter >> Page > |
Let’s investigate some examples that illustrate the relative magnitudes of the velocity, radius, and centripetal acceleration.
Solving for the radius, we find
Check Your Understanding A flywheel has a radius of 20.0 cm. What is the speed of a point on the edge of the flywheel if it experiences a centripetal acceleration of
134.0 cm/s
Centripetal acceleration can have a wide range of values, depending on the speed and radius of curvature of the circular path. Typical centripetal accelerations are given in the following table.
| Object | Centripetal Acceleration (m/s 2 or factors of g ) |
|---|---|
| Earth around the Sun | |
| Moon around the Earth | |
| Satellite in geosynchronous orbit | 0.233 |
| Outer edge of a CD when playing | |
| Jet in a barrel roll | (2–3 g ) |
| Roller coaster | (5 g ) |
| Electron orbiting a proton in a simple Bohr model of the atom |
A particle executing circular motion can be described by its position vector [link] shows a particle executing circular motion in a counterclockwise direction. As the particle moves on the circle, its position vector sweeps out the angle with the x- axis. Vector making an angle with the x- axis is shown with its components along the x - and y -axes. The magnitude of the position vector is and is also the radius of the circle, so that in terms of its components,
Here, is a constant called the angular frequency of the particle. The angular frequency has units of radians (rad) per second and is simply the number of radians of angular measure through which the particle passes per second. The angle that the position vector has at any particular time is .
If T is the period of motion, or the time to complete one revolution ( rad), then
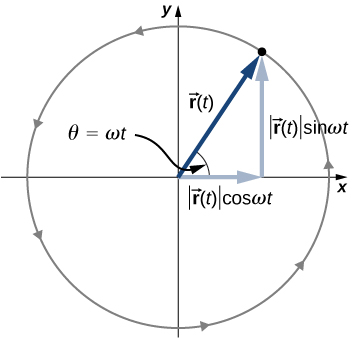
Velocity and acceleration can be obtained from the position function by differentiation:
It can be shown from [link] that the velocity vector is tangential to the circle at the location of the particle, with magnitude Similarly, the acceleration vector is found by differentiating the velocity:

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?