| << Chapter < Page | Chapter >> Page > |
A skater glides along a circular path of radius 5.00 m in clockwise direction. When he coasts around one-half of the circle, starting from the west point, find (a) the magnitude of his displacement vector and (b) how far he actually skated. (c) What is the magnitude of his displacement vector when he skates all the way around the circle and comes back to the west point?
a. 10.00 m, b. , c. 0
A stubborn dog is being walked on a leash by its owner. At one point, the dog encounters an interesting scent at some spot on the ground and wants to explore it in detail, but the owner gets impatient and pulls on the leash with force along the leash. (a) What is the magnitude of the pulling force? (b) What angle does the leash make with the vertical?
If the velocity vector of a polar bear is , how fast and in what geographic direction is it heading? Here, and are directions to geographic east and north, respectively.
22.2 km/h, south of west
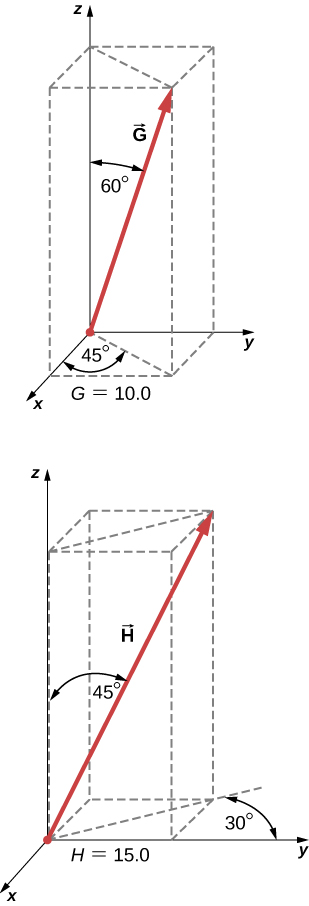
Find the scalar components of three-dimensional vectors and in the following figure and write the vectors in vector component form in terms of the unit vectors of the axes.
A diver explores a shallow reef off the coast of Belize. She initially swims 90.0 m north, makes a turn to the east and continues for 200.0 m, then follows a big grouper for 80.0 m in the direction north of east. In the meantime, a local current displaces her by 150.0 m south. Assuming the current is no longer present, in what direction and how far should she now swim to come back to the point where she started?
240.2 m, south of west
A force vector has x - and y -components, respectively, of −8.80 units of force and 15.00 units of force. The x - and y -components of force vector are, respectively, 13.20 units of force and −6.60 units of force. Find the components of force vector that satisfies the vector equation .
Vectors and are two orthogonal vectors in the xy -plane and they have identical magnitudes. If , find .
or
For the three-dimensional vectors in the following figure, find (a) , (b) , and (c) .

Show that is the volume of the parallelepiped, with edges formed by the three vectors in the following figure.
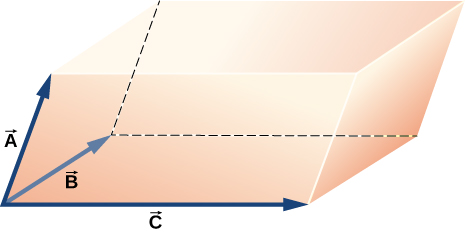
proof
Vector is 5.0 cm long and vector is 4.0 cm long. Find the angle between these two vectors when and .
What is the component of the force vector along the force vector ?
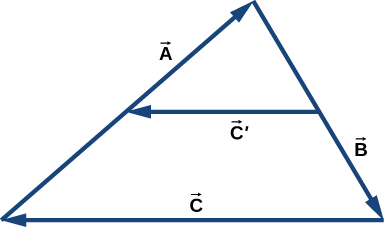
The following figure shows a triangle formed by the three vectors , , and . If vector is drawn between the midpoints of vectors and , show that .
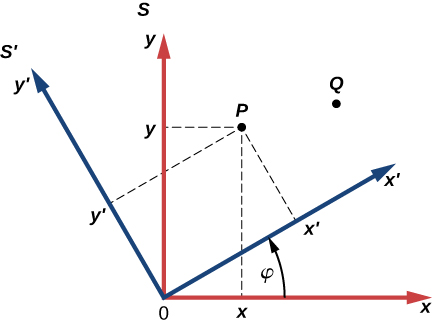
Distances between points in a plane do not change when a coordinate system is rotated. In other words, the magnitude of a vector is invariant under rotations of the coordinate system. Suppose a coordinate system S is rotated about its origin by angle to become a new coordinate system , as shown in the following figure. A point in a plane has coordinates ( x , y ) in S and coordinates in .
(a) Show that, during the transformation of rotation, the coordinates in are expressed in terms of the coordinates in S by the following relations:
(b) Show that the distance of point P to the origin is invariant under rotations of the coordinate system. Here, you have to show that
(c) Show that the distance between points P and Q is invariant under rotations of the coordinate system. Here, you have to show that
proof

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?