| << Chapter < Page | Chapter >> Page > |
By the definition of vector product, the torque is perpendicular to the plane formed by the position vector and force. Besides, it is also perpendicular to each of the two vectors individually. However, the vector relation by itself does not tell which side of the plane formed by operands is the direction of torque. In order to decide the orientation of the torque, we employ right hand vector product rule.
For this, we need to shift one of the operand vectors such that their tails meet at a point. It is convenient to shift the force vector, because application of right hand vector multiplication rule at the point (origin of the coordinate system) gives us the sense of angular direction of the torque.
Vector product
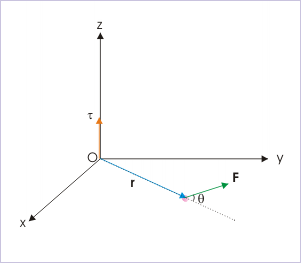
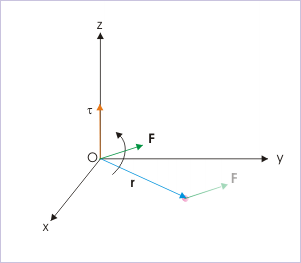
In the figure, we shift the second vector ( F ) so that tails of two operand vectors meet at the point (origin) about which torque is calculated. The two operand vectors define a plane ("xy" - plane in the figure). The torque ( τ ) is, then, acting along a line perpendicular to this plane and passing through the meeting point (origin).
The orientation of the torque vector in either of two direction is determined by applying right hand rule. For this, we sweep the closed fingers of the right hand from position vector (first vector) to force vector (second vector). The outstretched thumb, then, indicates the orientation of torque. In the case shown, the direction of torque is positive z-direction.
While interpreting the vector product, we must be careful about the sequence of operand. The vector product " " is negative or opposite in sign to that of " ".
The problem involving torque is about evaluating the vector product. We have the options of using any of the three methods described above for calculating the magnitude of torque. In this section, we shall work with two important aspects of calculating torque :
Here, we have two choices. Either, we evaluate torques for each force and then find the resultant torque or we evaluate the resultant (net) force first and then find the torque. The choice depends on the situation in hand.
In particular, if we find that the resulting torques are along the same direction (say one of the coordinate direction), then it is always better to calculate torque individually. This is because torques along a direction can be dealt as scalars with appropriate sign. The resultant torque is simply the algebraic sum. Example below highlights the this aspect.
The bottom line in making choice is that we should keep non-linear vector summation - whether that of force or torque - to a minimum. Otherwise, analytical technique for vector addition will be need to be employed.
Problem : At an instant, a particle in xy plane is acted by two forces 5 N and 10 N in xy plane as shown in the figure. Find the net torque on the particle at that instant.
Torque on a particle
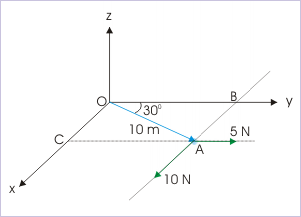
Solution : An inspection of the figure reveals that forces are parallel to axes and perpendicular linear distances of the lines of forces can be known. In this situation, calculation of the magnitude of torque suits to the form of expression that uses moment arm. Here, moment arms for two forces are :
For 5 N force, the moment arm "AB" is :
For 10 N force, the moment arm "AC" is :
The torques due to 5 N is :
The torques due to 10 N is :
Net torque is :

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?