18.1 Torque  (Page 6/3)

Torque about a point is a concept that denotes the tendency of force to turn or rotate an object in motion. This tendency is measured in general about a point. It is also termed as "moment of force". The torque in angular motion corresponds to force in translation. It is the "cause" whose effect is either angular acceleration or angular deceleration of a particle in general motion. Quantitatively, it is defined as a vector given by :

Rotation is a special case of angular motion. In the case of rotation, torque is defined with respect to an axis such that vector " r " is constrained to be perpendicular to the axis of rotation. In other words, the plane of motion is perpendicular to the axis of rotation. Clearly, the torque in rotation corresponds to force in translation.

Torque about a point

An external force on a particle constitutes a torque with respect to a point. Only condition is that the point, about which torque is defined or measured, does not lie on the line of force, in which case torque is zero.

Torque on a particle

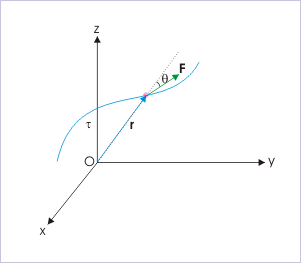
We can make note of the fact that it is convenient to construct reference system in such a manner so that the point (about which torque is measured) coincides with the origin. In that case, the vector ( r ) denoting the position of the particle with respect to point, becomes the position vector, which is measured from the origin of reference system.

Magnitude of torque

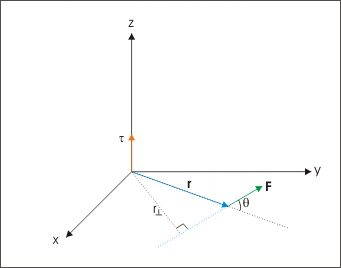
With the reference of origin for measuring torque, we can find the magnitude of torque, using any of the following relations given below. Here, we have purposely considered force in xy - plane for illustration and visualization purpose as it provides clear directional relationship of torque " τ " with the operand vectors " r " and " F ".

Torque on a particle

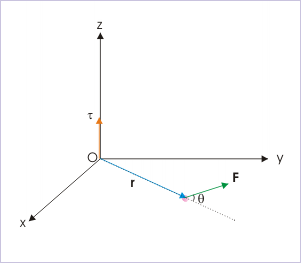
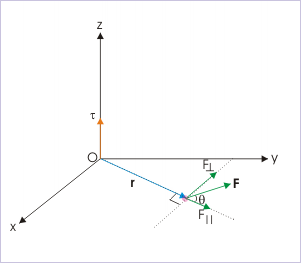
1: Torque in terms of angle enclosed

2: Torque in terms of force perpendicular to position vector

3: Torque in terms of moment arm

Torque on a particle

Problem : A projectile of mass "m" is projected with a speed "v" at an angle "θ" with the horizontal. Calculate the torque on the particle at the maximum height in relation to the point of projection.

Solution : The magnitude of the torque is given by :

Projectile motion

$$\begin{array}{l}\tau =r_{\perp }F=\mathrm{product\; of\; moment\; arm\; and\; magnitude\; of\; force}\end{array}$$

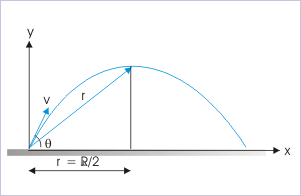
where $r\perp$ is moment arm. In this case, the moment arm is equal to half of the horizontal range of the flight,

$$\begin{array}{l}{r}_{\perp }=\frac{R}{2}=\frac{v^2\sin \mathrm{2\theta }}{2g}\end{array}$$

Now, the force on the projectile of mass "m" is due to the force of gravity :

$$\begin{array}{l}F=mg\end{array}$$

Putting these expressions of moment arm and force in the expression of torque, we have :

$$\begin{array}{l}\Rightarrow \tau =\frac{mg{v}^2\sin \mathrm{2\theta }}{2}\end{array}$$

Application of right hand rule indicates that torque is clockwise and is directed in to the page.

Got questions? Get instant answers now!

Direction of torque

The determination of torque's direction is relatively easier than that of angular velocity. The reason is simple. The torque itself is equal to vector product of two vectors, unlike angular velocity which is one of the two operands of the vector product. Clearly, if we know the directions of two operands here, the direction of torque can easily be interpreted.