Points, lines and angles  (Page 4/3)

Introduction

The purpose of this chapter is to recap some of the ideas that you learned in geometry and trigonometry in earlier grades. You should feel comfortable with the work covered in this chapter before attempting to move onto the Grade 10 Geometry Chapter or the Grade 10 Trigonometry Chapter . This chapter revises:

1. Terminology: quadrilaterals, vertices, sides, angles, parallel lines, perpendicular lines, diagonals, bisectors, transversals
2. Similarities and differences between quadrilaterals
3. Properties of triangles and quadrilaterals
4. Congruence
5. Classification of angles into acute, right, obtuse, straight, reflex or revolution
6. Theorem of Pythagoras which is used to calculate the lengths of sides of a right-angled triangle

Points and lines

The two simplest objects in geometry are points and lines .

A point is a coordinate that marks a position in space (on a number line, on a plane or in three dimensions or even more) and is denoted by a dot. Points are usually labelled with a capital letter. Some examples of how points can be represented are shown in [link] .

A line is a continuous set of coordinates in space and can be thought of as being formed when many points are placed next to each other. Lines can be straight or curved, but are always continuous. This means that there are never any breaks in the lines. The endpoints of lines are labelled with capital letters. Examples of two lines are shown in [link] .

Lines are labelled according to the start point and end point. We call the line that starts at a point $A$ and ends at a point $B$ , $AB$ . Since the line from point $B$ to point $A$ is the same as the line from point $A$ to point $B$ , we have that $AB=BA$ .

The length of the line between points $A$ and $B$ is $AB$ . So if we say $AB=CD$ we mean that the length of the line between $A$ and $B$ is equal to the length of the line between $C$ and $D$ .

A line is measured in units of length . Some common units of length are listed in [link] .

Angles

An angle is formed when two straight lines meet at a point. The point at which two lines meet is known as a vertex . Angles are labelled with a $\widehat{}$ called a caret on a letter. For example, in [link] the angle is at $\widehat{B}$ . Angles can also be labelled according to the line segments that make up the angle. For example, in [link] the angle is made up when line segments $CB$ and $BA$ meet. So, the angle can be referred to as $\angle CBA$ or $\angle ABC$ . The $\angle$ symbol is a short method of writing angle in geometry.

Angles are measured in degrees which is denoted by ${}^{\circ }$ , a small circle raised above the text in the same fashion as an exponent (or a superscript).

Measuring angles

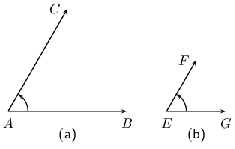
The size of an angle does not depend on the length of the lines that are joined to make up the angle, but depends only on how both the lines are placed as can be seen in [link] . This means that the idea of length cannot be used to measure angles. An angle is a rotation around the vertex.