| << Chapter < Page | Chapter >> Page > |
Angles are measured in degrees which is denoted by , a small circle raised above the text in the same fashion as an exponent (or a superscript).
Angles can also be measured in radians. At high school level you will only use degrees, but if you decide to take maths at university you will learn about radians.
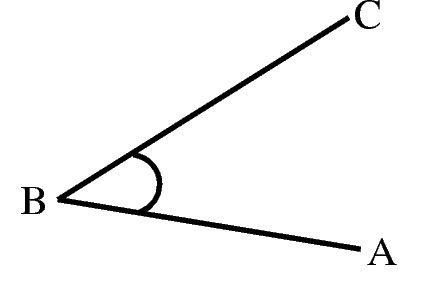
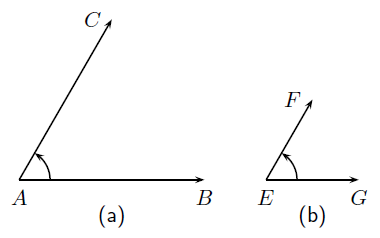
The size of an angle does not depend on the length of the lines that are joined to make up the angle, but depends only on how both the lines are placed as can be seen in [link] . This means that the idea of length cannot be used to measure angles. An angle is a rotation around the vertex.
A protractor is a simple tool that is used to measure angles. A picture of a protractor is shown in [link] .
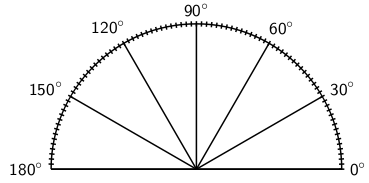
Method:
Using a protractor
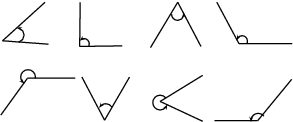
What is the smallest angle that can be drawn? The figure below shows two lines ( and ) making an angle at a common vertex . If line is rotated around the common vertex , down towards line , then the smallest angle that can be drawn occurs when the two lines are pointing in the same direction. This gives an angle of 0 . This is shown in [link]
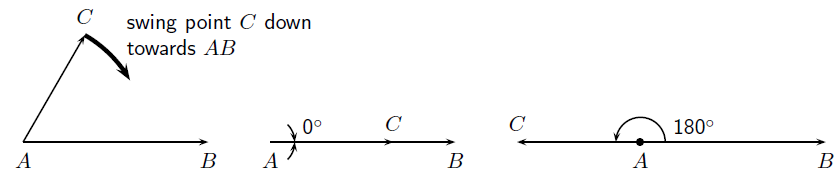
If line is now swung upwards, any other angle can be obtained. If line and line point in opposite directions (the third case in [link] ) then this forms an angle of 180 .
An angle of 90
is called a
right angle . A right angle is half the size of the angle made by a straight line (180
). We say
is
perpendicular to
or

All angles larger than 360 also look like we have seen them before. If you are given an angle that is larger than 360 , continue subtracting 360 from the angle, until you get an answer that is between 0 and 360 . Angles that measure more than 360 are largely for mathematical convenience.
These are simply labels for angles in particular ranges, shown in [link] .

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 maths [caps]' conversation and receive update notifications?