1. Home
  2. Algebra i for the community
  3. Chapter 5: exponents and
  4. Chapter 5 part y
  5. Multiplication of polynomials

Multiplication of polynomials

<< Chapter < Page
  Algebra i for the community     Page 1 / 2
Chapter >> Page >
This module is from Elementary Algebra by Denny Burzynski and Wade Ellis, Jr. Operations with algebraic expressions and numerical evaluations are introduced in this chapter. Coefficients are described rather than merely defined. Special binomial products have both literal and symbolic explanations and since they occur so frequently in mathematics, we have been careful to help the student remember them. In each example problem, the student is "talked" through the symbolic form.Objectives of this module: be able to multiply a polynomial by a monomial, be able to simplify +(a + b) and -(a - b), be able to multiply a polynomial by a polynomial.

Overview

  • Multiplying a Polynomial by a Monomial
  • Simplifying + ( a + b ) and − ( a + b )
  • Multiplying a Polynomial by a Polynomial

Multiplying a polynomial by a monomial

Multiplying a polynomial by a monomial is a direct application of the distributive property.

Distributive property

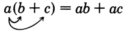
The product of a monomial a and a binomial b plus c is equal to ab plus ac. This is the distributive property. In the expression, there are two arrows originating from the monomial, a, and pointing towards the terms b and c of the binomial.

The distributive property suggests the following rule.

Multiplying a polynomial by a monomial

To multiply a polynomial by a monomial, multiply every term of the polynomial by the monomial and then add the resulting products together.

Sample set a

Finding the product of three and the binomial 'x plus nine', using the distributive property. See the longdesc for a full description.
Finding the product of six and the binomial 'x cubed minus two x,' using the distributive property. See the longdesc for a full description.
Finding the product of the binomial 'x minus seven' and 'x', using the distributive property. See the longdesc for a full description.
Finding the product of 'eight a squared' and the trinomial 'three a to the fourth power minus five a cubed plus a,' using the distributive property. See the longdesc for a full description.
Finding the product of 'four x squared y to the seventh power z' and the binomial 'x to the fifth power y plus eight y squared z squared,' using the distributive property. See the longdesc for a full description.

10 a b 2 c ( 125 a 2 ) = 1250 a 3 b 2 c

Finding the product of the binomial 'nine x squared z plus four w' and the product of 'five z and w cubed,' using the distributive property. See the longdesc for a full description.

Practice set a

Determine the following products.

3 ( x + 8 )

3 x + 24

( 2 + a ) 4

4 a + 8

( a 2 − 2 b + 6 ) 2 a

2 a 3 − 4 a b + 12 a

8 a 2 b 3 ( 2 a + 7 b + 3 )

16 a 3 b 3 + 56 a 2 b 4 + 24 a 2 b 3

4 x ( 2 x 5 + 6 x 4 − 8 x 3 − x 2 + 9 x − 11 )

8 x 6 + 24 x 5 − 32 x 4 − 4 x 3 + 36 x 2 − 44 x

( 3 a 2 b ) ( 2 a b 2 + 4 b 3 )

6 a 3 b 3 + 12 a 2 b 4

5 m n ( m 2 n 2 + m + n 0 ) ,       n ≠ 0

5 m 3 n 3 + 5 m 2 n + 5 m n

Use a calculator. 6.03 ( 2.11 a 3 + 8.00 a 2 b )

12.7233 a 3 + 48.24 a 2 b

Simplifying + ( a + b ) And - ( a + b )

+ ( a + b ) And - ( a + b )

Oftentimes, we will encounter multiplications of the form

+ 1 ( a + b ) or - 1 ( a + b )

These terms will actually appear as

+ ( a + b ) and - ( a + b )

Using the distributive property, we can remove the parentheses.

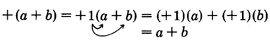
Removal of a set of parentheses preceded by a plus sign using the distributive property. See the longdesc for a full description.

The parentheses have been removed and the sign of each term has remained the same.

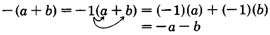
Removal of a set of parentheses preceded by a minus sign using the distributive property. See the longdesc for a full description.

The parentheses have been removed and the sign of each term has been changed to its opposite.

  1. To remove a set of parentheses preceded by a " + " sign, simply remove the parentheses and leave the sign of each term the same.
  2. To remove a set of parentheses preceded by a “ − ” sign, remove the parentheses and change the sign of each term to its opposite sign.

Sample set b

Simplify the expressions.

( 6 x − 1 ) .

This set of parentheses is preceded by a “ + ’’ sign (implied). We simply drop the parentheses.

( 6 x − 1 ) = 6 x − 1

( 14 a 2 b 3 − 6 a 3 b 2 + a b 4 ) = 14 a 2 b 3 − 6 a 3 b 2 + a b 4

− ( 21 a 2 + 7 a − 18 ) .

This set of parentheses is preceded by a “ − ” sign. We can drop the parentheses as long as we change the sign of every term inside the parentheses to its opposite sign.

− ( 21 a 2 + 7 a − 18 ) = − 21 a 2 − 7 a + 18

− ( 7 y 3 − 2 y 2 + 9 y + 1 ) = − 7 y 3 + 2 y 2 − 9 y − 1

Practice set b

Simplify by removing the parentheses.

( 2 a + 3 b )

2 a + 3 b

( a 2 − 6 a + 10 )

a 2 − 6 a + 10

− ( x + 2 y )

− x − 2 y

− ( 5 m − 2 n )

− 5 m + 2 n

− ( − 3 s 2 − 7 s + 9 )

3 s 2 + 7 s − 9

Multiplying a polynomial by a polynomial

Since we can consider an expression enclosed within parentheses as a single quantity, we have, by the distributive property,

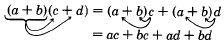
Finding the product of the binomials 'a plus b' and 'c plus d', using the distributive property. See the longdesc for a full description.

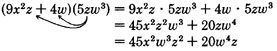
For convenience we will use the commutative property of addition to write this expression so that the first two terms contain a and the second two contain b .
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Algebra i for the community college. OpenStax CNX. Dec 19, 2014 Download for free at http://legacy.cnx.org/content/col11598/1.3
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Algebra i for the community college' conversation and receive update notifications?

Ask