1. Home
  2. Algebra i for the community
  3. Chapter 5: exponents and
  4. Chapter 5 part y
  5. Special products

8.1 Special products

<< Chapter < Page
  Algebra i for the community   Page 1 / 1
Chapter >> Page >
This module is from Elementary Algebra by Denny Burzynski and Wade Ellis, Jr. Operations with algebraic expressions and numerical evaluations are introduced in this chapter. Coefficients are described rather than merely defined. Special binomial products have both literal and symbolic explanations and since they occur so frequently in mathematics, we have been careful to help the student remember them. In each example problem, the student is "talked" through the symbolic form.Objectives of this module: be able to expand (a + b)^2, (a - b)^2, and (a + b)(a - b).

Overview

  • Expanding ( a + b ) 2 and ( a − b ) 2
  • Expanding ( a + b ) ( a − b )

Three binomial products occur so frequently in algebra that we designate them as special binomial products . We have seen them before (Sections [link] and [link] ), but we will study them again because of their importance as time saving devices and in solving equations (which we will study in a later chapter).

These special products can be shown as the squares of a binomial

( a + b ) 2      and      ( a − b ) 2

and as the sum and difference of two terms .

( a + b ) ( a − b )

There are two simple rules that allow us to easily expand (multiply out) these binomials. They are well worth memorizing, as they will save a lot of time in the future.

Expanding ( a + b ) 2 And ( a − b ) 2

Squaring a binomial

To square a binomial: *

  1. Square the first term.
  2. Take the product of the two terms and double it.
  3. Square the last term.
  4. Add the three results together.

( a + b ) 2 = a 2 + 2 a b + b 2 ( a − b ) 2 = a 2 − 2 a b + b 2

Expanding ( a + b ) ( a − b )

Sum and difference of two terms

To expand the sum and difference of two terms: †

  1. Square the first term and square the second term.
  2. Subtract the square of the second term from the square of the first term.

( a + b ) ( a − b ) = a 2 − b 2


* See problems 56 and 57 at the end of this section.
† See problem 58.

Sample set a

( x + 4 ) 2 Square   the   first   term:    x 2 . The   product   of   both   terms   is   4 x .   Double   it:    8 x . Square   the   last   term:   16 . Add   them   together:    x 2 + 8 x + 16. ( x + 4 ) 2 = x 2 + 8 x + 16

Note that ( x + 4 ) 2 ≠ x 2 + 4 2 . The 8 x term is missing!

( a − 8 ) 2 Square   the   first   term:    a 2 . The   product   of   both   terms   is − 8 a .   Double   it:    − 16 a . Square   the   last   term:    64. Add   them   together:    a 2 + ( − 16 a ) + 64. ( a − 8 ) 2 = a 2 − 16 a + 64

Notice that the sign of the last term in this expression is “ + .” This will always happen since the last term results from a number being squared . Any nonzero number times itself is always positive.

( + ) ( + ) = +      and      ( − ) ( − ) = +

The sign of the second term in the trinomial will always be the sign that occurs inside the parentheses.

( y − 1 ) 2 Square   the   first   term:    y 2 . The   product   of   both   terms   is − y .   Double   it:    − 2 y . Square   the   last   term:    + 1. Add   them   together:    y 2 + ( − 2 y ) + 1.

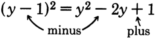
The square of the binomial 'y minus one' is equal to y squared minus two y plus one. The sign inside the parentheses and the sign of the middle term of the trinomial are the same, and are labeled as 'minus.' The sign of the last term of the trinomial is labeled as 'plus.'

( 5 x + 3 ) 2 Square   the   first   term:    25 x 2 . The   product   of   both   terms   is 15 x .   Double   it:    30 x . Square   the   last   term:   9 . Add   them   together:    25 x 2 + 30 x + 9.

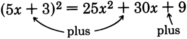
The square of the binomial 'five x plus three' is equal to twenty five x squared plus thirty x plus nine. The sign inside the parentheses and the sign of the middle term of the trinomial are the same, and are labeled as 'plus.' The sign of the last term of the trinomial is also labeled as 'plus.'

( 7 b − 2 ) 2 Square   the   first   term:    49 b 2 . The   product   of   both   terms   is   − 14 b .   Double   it:    − 28 b . Square   the   last   term:   4 . Add   them   together:    49 b 2 + ( − 28 b ) + 4.

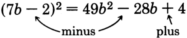
The square of the binomial 'seven b minus two' is equal to forty-nine b squared minus twenty-eight b plus four. The sign inside the parentheses and the sign of the middle term of the trinomial are the same, and are labeled as 'minus.' The sign of the last term of the trinomial is labeled as 'plus.'

( x + 6 ) ( x − 6 ) Square   the   first   term:           x 2 . Subtract   the   square   of   the   second   term   ( 36 )   from the   square   of   the   first   term:         x 2 − 36. ( x + 6 ) ( x − 6 ) = x 2 − 36

( 4 a − 12 ) ( 4 a + 12 ) Square   the   first   term:           16 a 2 . Subtract   the   square   of   the   second   term   ( 144 )   from the   square   of   the   first   term:         16 a 2 − 144. ( 4 a − 12 ) ( 4 a + 12 ) = 16 a 2 − 144

( 6 x + 8 y ) ( 6 x − 8 y ) Square   the   first   term:           36 x 2 . Subtract   the   square   of   the   second   term   ( 64 y 2 )   from the   square   of   the   first   term:         36 x 2 − 64 y 2 . ( 6 x + 8 y ) ( 6 x − 8 y ) = 36 x 2 − 64 y 2

Practice set a

Find the following products.

( x + 5 ) 2

x 2 + 10 x + 25

( x + 7 ) 2

x 2 + 14 x + 49

( y − 6 ) 2

y 2 − 12 y + 36

( 3 a + b ) 2

9 a 2 + 6 a b + b 2

( 9 m − n ) 2

81 m 2 − 18 m n + n 2

( 10 x − 2 y ) 2

100 x 2 − 40 x y + 4 y 2

( 12 a − 7 b ) 2

144 a 2 − 168 a b + 49 b 2

( 5 h − 15 k ) 2

25 h 2 − 150 h k + 225 k 2

Exercises

For the following problems, find the products.

( x + 3 ) 2

x 2 + 6 x + 9

( x + 5 ) 2

( x + 8 ) 2

x 2 + 16 x + 64

( x + 6 ) 2

( y + 9 ) 2

y 2 + 18 y + 81

( y + 1 ) 2

( a − 4 ) 2

a 2 − 8 a + 16

( a − 6 ) 2

( a − 7 ) 2

a 2 − 14 a + 49

( b + 10 ) 2

( b + 15 ) 2

b 2 + 30 b + 225

( a − 10 ) 2

( x − 12 ) 2

x 2 − 24 x + 144

( x + 20 ) 2

( y − 20 ) 2

y 2 − 40 y + 400

( 3 x + 5 ) 2

( 4 x + 2 ) 2

16 x 2 + 16 x + 4

( 6 x − 2 ) 2

( 7 x − 2 ) 2

49 x 2 − 28 x + 4

( 5 a − 6 ) 2

( 3 a − 9 ) 2

9 a 2 − 54 a + 81

( 3 w − 2 z ) 2

( 5 a − 3 b ) 2

25 a 2 − 30 a b + 9 b 2

( 6 t − 7 s ) 2

( 2 h − 8 k ) 2

4 h 2 − 32 h k + 64 k 2

( a + 1 2 ) 2

( a + 1 3 ) 2

a 2 + 2 3 a + 1 9

( x + 3 4 ) 2

( x + 2 5 ) 2

x 2 + 4 5 x + 4 25

( x − 2 3 ) 2

( y − 5 6 ) 2

y 2 − 5 3 y + 25 36

( y + 2 3 ) 2

( x + 1.3 ) 2

x 2 + 2.6 x + 1.69

( x + 5.2 ) 2

( a + 0.5 ) 2

a 2 + a + 0.25

( a + 0.08 ) 2

( x − 3.1 ) 2

x 2 − 6.2 x + 9.61

( y − 7.2 ) 2

( b − 0.04 ) 2

b 2 − 0.08 b + 0.0016

( f − 1.006 ) 2

( x + 5 ) ( x − 5 )

x 2 − 25

( x + 6 ) ( x − 6 )

( x + 1 ) ( x − 1 )

x 2 − 1

( t − 1 ) ( t + 1 )

( f + 9 ) ( f − 9 )

f 2 − 81

( y − 7 ) ( y + 7 )

( 2 y + 3 ) ( 2 y − 3 )

4 y 2 − 9

( 5 x + 6 ) ( 5 x − 6 )

( 2 a − 7 b ) ( 2 a + 7 b )

4 a 2 − 49 b 2

( 7 x + 3 t ) ( 7 x − 3 t )

( 5 h − 2 k ) ( 5 h + 2 k )

25 h 2 − 4 k 2

( x + 1 3 ) ( x − 1 3 )

( a + 2 9 ) ( a − 2 9 )

a 2 − 4 81

( x + 7 3 ) ( x − 7 3 )

( 2 b + 6 7 ) ( 2 b − 6 7 )

4 b 2 − 36 49

Expand ( a + b ) 2 to prove it is equal to a 2 + 2 a b + b 2 .

Expand ( a − b ) 2 to prove it is equal to a 2 − 2 a b + b 2 .

( a − b ) ( a − b ) = a 2 − a b − a b + b 2 = a 2 − 2 a b + b 2

Expand ( a + b ) ( a − b ) to prove it is equal to a 2 − b 2 .

Fill in the missing label in the equation below.

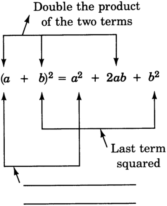
The square of the binomial 'a plus b' is equal to a squared plus two ab plus b squared. Fill in the missing labels for the equation. See the longdesc for a full description.

first term squared

Label the parts of the equation below.

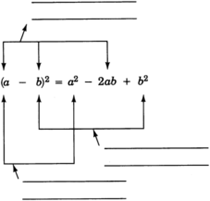
The square of the binomial 'a minus b' is equal to a squared minus two ab plus b squared. Fill in the missing labels for the equation. See the longdesc for a full description.

Label the parts of the equation below.

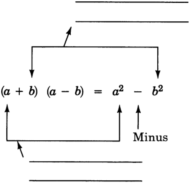
The product of the binomial 'a plus b' and the binomial 'a minus b' is equal to a squared minus b squared. Fill in the missing labels for the equation. See the longdesc for a full description.

(a) Square the first term.
(b) Square the second term and subtract it from the first term.

Exercises for review

( [link] ) Simplify ( x 3 y 0 z 4 ) 5 .

( [link] ) Find the value of 10 − 1 ⋅ 2 − 3 .

1 80

( [link] ) Find the product. ( x + 6 ) ( x − 7 ) .

( [link] ) Find the product. ( 5 m − 3 ) ( 2 m + 3 ) .

10 m 2 + 9 m − 9

( [link] ) Find the product. ( a + 4 ) ( a 2 − 2 a + 3 ) .
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Algebra i for the community college. OpenStax CNX. Dec 19, 2014 Download for free at http://legacy.cnx.org/content/col11598/1.3
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Algebra i for the community college' conversation and receive update notifications?

Ask