This module is from Elementary Algebra by Denny Burzynski and Wade Ellis, Jr.
Operations with algebraic expressions and numerical evaluations are introduced in this chapter. Coefficients are described rather than merely defined. Special binomial products have both literal and symbolic explanations and since they occur so frequently in mathematics, we have been careful to help the student remember them. In each example problem, the student is "talked" through the symbolic form.Objectives of this module: understand the concept of like terms, be able to combine like terms, be able to simplify expressions containing parentheses.
Overview
- Like Terms
- Combining Like Terms
- Simplifying Expressions Containing Parentheses
Like terms
Like terms
Terms whose variable parts, including the exponents, are identical are called
like terms . Like terms is an appropriate name since terms with identical variable parts and different numerical coefficients represent different amounts of the same quantity. As long as we are dealing with quantities of the same type we can combine them using addition and subtraction.
Simplifying an algebraic expression
An algebraic expression can be
simplified by combining like terms.
Sample set a
Combine the like terms.
. 6 and 4 of the same type give 10 of that type.
. 6 and 4 of the same type give 10 of that type. Thus, we have 10 of one type and 2 of another type.
Suppose we let the letter
represent "house." Then,
. 6 and 4 of the same type give 10 of that type.
Suppose we let
represent "house" and
represent "motel."
Practice set a
Like terms with the same numerical coefficient represent equal amounts of the same quantity.
Like terms with different numerical coefficients represent
.
different amounts of the same quantity
Combining like terms
Since like terms represent amounts of the same quantity, they may be combined, that is, like terms may be added together.
Sample set b
Simplify each of the following polynomials by combining like terms.
.
There are
, then 5 more, then 3 more. This makes a total of
.
.
From
, we lose
. This makes
. The
represent a quantity different from the
and therefore will not combine with them.
.
and
represent quantities of the same type.
and
represent quantities of the same type.
Thus,
Practice set b
Simplify each of the following expressions.
Simplifying expressions containing parentheses
Simplifying expressions containing parentheses
When parentheses occur in expressions, they must be removed before the expression can be simplified. Parentheses can be removed using the distributive property.
Distributive property
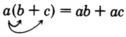
Sample set c
Simplify each of the following expressions by using the distributive property and combining like terms.
