7.3 Applications  (Page 24/13)

We saw in the chapter introduction that second-order linear differential equations are used to model many situations in physics and engineering. In this section, we look at how this works for systems of an object with mass attached to a vertical spring and an electric circuit containing a resistor, an inductor, and a capacitor connected in series. Models such as these can be used to approximate other more complicated situations; for example, bonds between atoms or molecules are often modeled as springs that vibrate, as described by these same differential equations.

Simple harmonic motion

Consider a mass suspended from a spring attached to a rigid support. (This is commonly called a spring-mass system .) Gravity is pulling the mass downward and the restoring force of the spring is pulling the mass upward. As shown in [link] , when these two forces are equal, the mass is said to be at the equilibrium position. If the mass is displaced from equilibrium, it oscillates up and down. This behavior can be modeled by a second-order constant-coefficient differential equation.

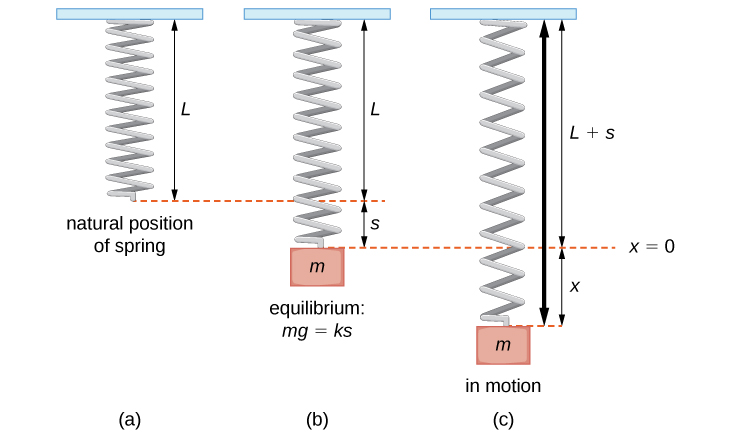
Let $x(t)$ denote the displacement of the mass from equilibrium. Note that for spring-mass systems of this type, it is customary to adopt the convention that down is positive. Thus, a positive displacement indicates the mass is below the equilibrium point, whereas a negative displacement indicates the mass is above equilibrium. Displacement is usually given in feet in the English system or meters in the metric system.

Consider the forces acting on the mass. The force of gravity is given by $mg\text{.}$ In the English system, mass is in slugs and the acceleration resulting from gravity is in feet per second squared. The acceleration resulting from gravity is constant, so in the English system, $g=32$ ft/sec ² . Recall that 1 slug-foot/sec ² is a pound, so the expression mg can be expressed in pounds. Metric system units are kilograms for mass and m/sec ² for gravitational acceleration. In the metric system, we have $g=9.8$ m/sec ² .

According to Hooke’s law , the restoring force of the spring is proportional to the displacement and acts in the opposite direction from the displacement, so the restoring force is given by $\text{−}k\left(s+x\right).$ The spring constant is given in pounds per foot in the English system and in newtons per meter in the metric system.

Now, by Newton’s second law, the sum of the forces on the system (gravity plus the restoring force) is equal to mass times acceleration, so we have

However, by the way we have defined our equilibrium position, $mg=ks,$ the differential equation becomes