7.2 Thermal expansion of solids and liquids  (Page 3/10)

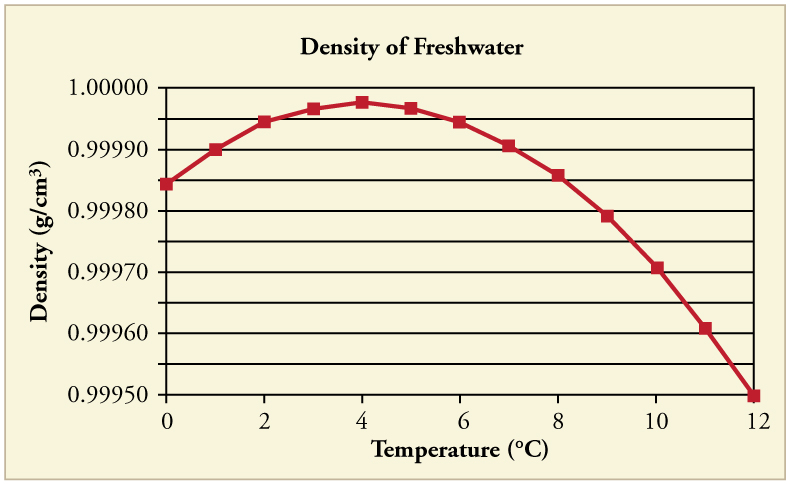
In general, objects will expand with increasing temperature. Water is the most important exception to this rule. Water expands with increasing temperature (its density decreases ) when it is at temperatures greater than $4\text{º}\text{C}(\text{40}\text{º}\text{F})$ . However, it expands with decreasing temperature when it is between $+4\text{º}\text{C}$ and $0\text{º}\text{C}$ $(\text{40}\text{º}\text{F}$ to $\text{32}\text{º}\text{F})$ . Water is densest at $+4\text{º}\text{C}$ . (See [link] .) Perhaps the most striking effect of this phenomenon is the freezing of water in a pond. When water near the surface cools down to $4\text{º}\text{C}$ it is denser than the remaining water and thus will sink to the bottom. This “turnover” results in a layer of warmer water near the surface, which is then cooled. Eventually the pond has a uniform temperature of $4\text{º}\text{C}$ . If the temperature in the surface layer drops below $4\text{º}\text{C}$ , the water is less dense than the water below, and thus stays near the top. As a result, the pond surface can completely freeze over. The ice on top of liquid water provides an insulating layer from winter’s harsh exterior air temperatures. Fish and other aquatic life can survive in $4\text{º}\text{C}$ water beneath ice, due to this unusual characteristic of water. It also produces circulation of water in the pond that is necessary for a healthy ecosystem of the body of water.

Making connections: real-world connections—filling the tank

Differences in the thermal expansion of materials can lead to interesting effects at the gas station. One example is the dripping of gasoline from a freshly filled tank on a hot day. Gasoline starts out at the temperature of the ground under the gas station, which is cooler than the air temperature above. The gasoline cools the steel tank when it is filled. Both gasoline and steel tank expand as they warm to air temperature, but gasoline expands much more than steel, and so it may overflow.

This difference in expansion can also cause problems when interpreting the gasoline gauge. The actual amount (mass) of gasoline left in the tank when the gauge hits “empty” is a lot less in the summer than in the winter. The gasoline has the same volume as it does in the winter when the “add fuel” light goes on, but because the gasoline has expanded, there is less mass. If you are used to getting another 40 miles on “empty” in the winter, beware—you will probably run out much more quickly in the summer.