1. Home
  2. College physics ii
  3. Temperature, kinetic theory,
  4. Thermal expansion of solids and

7.2 Thermal expansion of solids and liquids  (Page 2/10)

<< Chapter < Page
  College physics ii     Page 2 / 10
Chapter >> Page >
Thermal expansion coefficients at 20 º C size 12{"20"°C} {} Values for liquids and gases are approximate.
Material Coefficient of linear expansion α ( 1 / º C ) size 12{α \( 1/°C \) } {} Coefficient of volume expansion β ( 1 / º C ) size 12{β \( 1/°C \) } {}
Solids
Aluminum 25 × 10 – 6 size 12{"25" times "10" rSup { size 8{–6} } } {} 75 × 10 – 6 size 12{"75"´"10" rSup { size 8{ +- 6} } } {}
Brass 19 × 10 – 6 size 12{"19" times "10" rSup { size 8{–6} } } {} 56 × 10 – 6 size 12{"56"´"10" rSup { size 8{ +- 6} } } {}
Copper 17 × 10 – 6 size 12{"17" times "10" rSup { size 8{–6} } } {} 51 × 10 – 6 size 12{"51" times "10" rSup { size 8{–6} } } {}
Gold 14 × 10 – 6 size 12{"14" times "10" rSup { size 8{–6} } } {} 42 × 10 – 6 size 12{"42" times "10" rSup { size 8{–6} } } {}
Iron or Steel 12 × 10 – 6 size 12{"12" times "10" rSup { size 8{–6} } } {} 35 × 10 – 6 size 12{"35" times "10" rSup { size 8{–6} } } {}
Invar (Nickel-iron alloy) 0 . 9 × 10 – 6 size 12{0 "." 9 times "10" rSup { size 8{–6} } } {} 2 . 7 × 10 – 6 size 12{2 "." 7 times "10" rSup { size 8{–6} } } {}
Lead 29 × 10 – 6 size 12{"29" times "10" rSup { size 8{–6} } } {} 87 × 10 – 6 size 12{"87" times "10" rSup { size 8{–6} } } {}
Silver 18 × 10 – 6 size 12{"18" times "10" rSup { size 8{–6} } } {} 54 × 10 – 6 size 12{"54" times "10" rSup { size 8{–6} } } {}
Glass (ordinary) 9 × 10 – 6 size 12{9 times "10" rSup { size 8{–6} } } {} 27 × 10 – 6 size 12{"27" times "10" rSup { size 8{–6} } } {}
Glass (Pyrex®) 3 × 10 – 6 size 12{3 times "10" rSup { size 8{–6} } } {} 9 × 10 – 6 size 12{9 times "10" rSup { size 8{–6} } } {}
Quartz 0 . 4 × 10 – 6 size 12{0 "." 4´"10" rSup { size 8{ +- 6} } } {} 1 × 10 – 6 size 12{1 times "10" rSup { size 8{–6} } } {}
Concrete, Brick ~ 12 × 10 – 6 size 12{ "~" "12"´"10" rSup { size 8{ +- 6} } } {} ~ 36 × 10 – 6 size 12{ "~" "36" times "10" rSup { size 8{–6} } } {}
Marble (average) 7 × 10 – 6 size 12{2 "." 5´"10" rSup { size 8{ +- 6} } } {} 2 . 1 × 10 – 5 size 12{7 "." 5 times "10" rSup { size 8{–6} } } {}
Liquids
Ether 1650 × 10 – 6 size 12{"1650" times "10" rSup { size 8{–6} } } {}
Ethyl alcohol 1100 × 10 – 6 size 12{"1100" times "10" rSup { size 8{–6} } } {}
Petrol 950 × 10 – 6 size 12{"950" times "10" rSup { size 8{–6} } } {}
Glycerin 500 × 10 – 6 size 12{"500" times "10" rSup { size 8{–6} } } {}
Mercury 180 × 10 – 6 size 12{"180" times "10" rSup { size 8{–6} } } {}
Water 210 × 10 – 6 size 12{"210" times "10" rSup { size 8{–6} } } {}
Gases
Air and most other gases at atmospheric pressure 3400 × 10 – 6 size 12{"3400" times "10" rSup { size 8{–6} } } {}

Calculating linear thermal expansion: the golden gate bridge

The main span of San Francisco’s Golden Gate Bridge is 1275 m long at its coldest. The bridge is exposed to temperatures ranging from – 15 º C size 12{–"15"°C} {} to 40 º C size 12{"40"°C} {} . What is its change in length between these temperatures? Assume that the bridge is made entirely of steel.

Strategy

Use the equation for linear thermal expansion Δ L = αL Δ T size 12{ΔL=αL`ΔT} {} to calculate the change in length , Δ L size 12{ΔL} {} . Use the coefficient of linear expansion, α size 12{α} {} , for steel from [link] , and note that the change in temperature, Δ T size 12{ΔT} {} , is 55 º C size 12{"55"°C} {} .

Solution

Plug all of the known values into the equation to solve for Δ L size 12{ΔL} {} .

Δ L = αL Δ T = 12 × 10 − 6 º C 1275 m 55 º C = 0 . 84 m. size 12{ΔL=αLΔT= left ( { {"12" times "10" rSup { size 8{ - 6} } } over {°C} } right ) left ("1275 m" right ) left ("55"°C right )=0 "." "84 m"} {}

Discussion

Although not large compared with the length of the bridge, this change in length is observable. It is generally spread over many expansion joints so that the expansion at each joint is small.

Thermal expansion in two and three dimensions

Objects expand in all dimensions, as illustrated in [link] . That is, their areas and volumes, as well as their lengths, increase with temperature. Holes also get larger with temperature. If you cut a hole in a metal plate, the remaining material will expand exactly as it would if the plug was still in place. The plug would get bigger, and so the hole must get bigger too. (Think of the ring of neighboring atoms or molecules on the wall of the hole as pushing each other farther apart as temperature increases. Obviously, the ring of neighbors must get slightly larger, so the hole gets slightly larger).

Thermal expansion in two dimensions

For small temperature changes, the change in area Δ A size 12{ΔA} {} is given by

Δ A = 2 αA Δ T , size 12{ΔA=2αAΔT} {}

where Δ A size 12{ΔA} {} is the change in area A size 12{A} {} , Δ T size 12{ΔT} {} is the change in temperature, and α size 12{α} {} is the coefficient of linear expansion, which varies slightly with temperature.

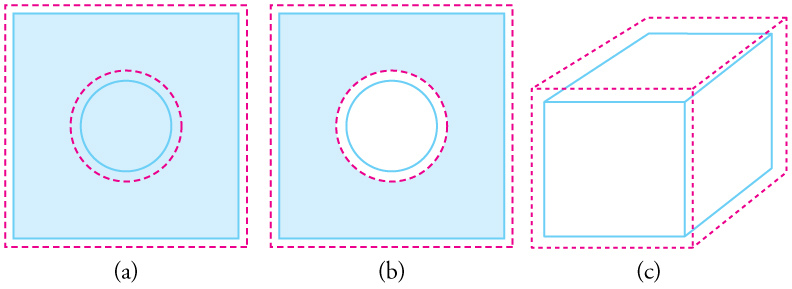
Part a shows the outline of a flat metal plate before and after expansion. After expansion, it has the same shape and ratio of dimensions as before, but it takes up a greater area. Part b shows the outline of a flat metal plate with a hole in it, before and after expansion. The hole expands. Part c shows the outline of a rectangular box before and after expansion. After expansion, the box has the same proportions as before expansion, but it has a greater volume.
In general, objects expand in all directions as temperature increases. In these drawings, the original boundaries of the objects are shown with solid lines, and the expanded boundaries with dashed lines. (a) Area increases because both length and width increase. The area of a circular plug also increases. (b) If the plug is removed, the hole it leaves becomes larger with increasing temperature, just as if the expanding plug were still in place. (c) Volume also increases, because all three dimensions increase.

Thermal expansion in three dimensions

The change in volume Δ V size 12{ΔV} {} is very nearly Δ V = 3 α V Δ T size 12{ΔV=3αVΔT} {} . This equation is usually written as

Δ V = βV Δ T , size 12{ΔV=βVΔT} {}

where β size 12{β} {} is the coefficient of volume expansion    and β ≈ 3α size 12{β approx 3α} {} . Note that the values of β size 12{β} {} in [link] are almost exactly equal to 3α size 12{3α} {} .
<< Chapter < Page Page > Chapter >>
Practice Key Terms 4

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, College physics ii. OpenStax CNX. Nov 29, 2012 Download for free at http://legacy.cnx.org/content/col11458/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'College physics ii' conversation and receive update notifications?

Ask