6.8 Quantum numbers and rules  (Page 2/10)

What are the allowed directions?

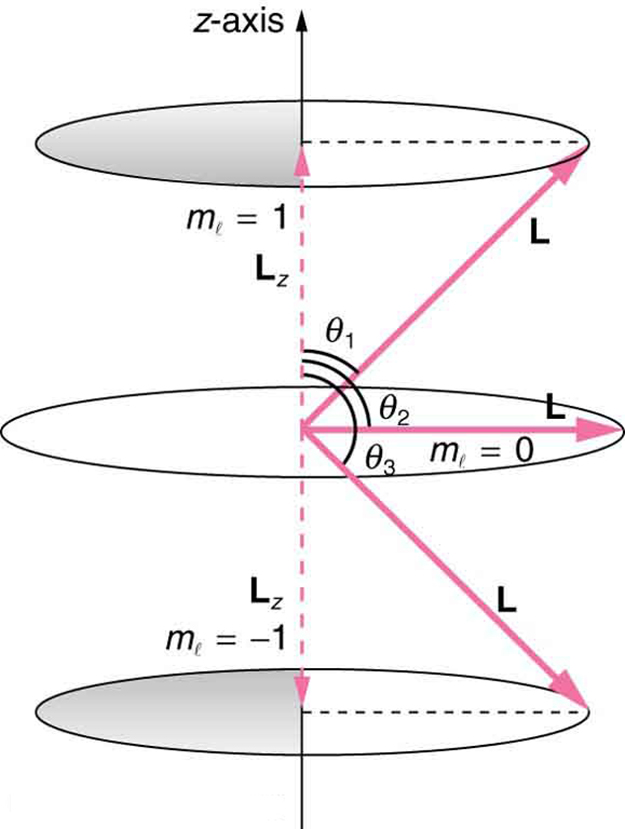
Calculate the angles that the angular momentum vector $\mathbf{\text{L}}$ can make with the $z$ -axis for $l=1$ , as illustrated in [link] .

Strategy

[link] represents the vectors $\mathbf{\text{L}}$ and ${\mathbf{\text{L}}}_z$ as usual, with arrows proportional to their magnitudes and pointing in the correct directions. $\mathbf{\text{L}}$ and ${\mathbf{\text{L}}}_z$ form a right triangle, with $\mathbf{L}$ being the hypotenuse and ${\mathbf{\text{L}}}_z$ the adjacent side. This means that the ratio of ${\mathbf{L}}_z$ to $\mathbf{L}$ is the cosine of the angle of interest. We can find $\mathbf{\text{L}}$ and ${\mathbf{\text{L}}}_z$ using $L=\sqrt{l\left(l+1\right)}\frac{h}{\mathrm{2\pi }}$ and $L_z=m\frac{h}{\mathrm{2\pi }}$ .

Solution

We are given $l=1$ , so that $m_l$ can be +1, 0, or −1. Thus $L$ has the value given by $L=\sqrt{l\left(l+1\right)}\frac{h}{\mathrm{2\pi }}$ .

$L_z$ can have three values, given by $L_z=m_l\frac{h}{\mathrm{2\pi }}$ .

As can be seen in [link] , $\cos \theta ={\text{L}}_z\text{/L,}$ and so for $m_l=+1$ , we have

Thus,

Similarly, for $m_l=0$ , we find $\text{cos}{\theta }_2=0$ ; thus,

And for $m_l=-1$ ,

so that

Discussion

The angles are consistent with the figure. Only the angle relative to the $z$ -axis is quantized. $L$ can point in any direction as long as it makes the proper angle with the $z$ -axis. Thus the angular momentum vectors lie on cones as illustrated. This behavior is not observed on the large scale. To see how the correspondence principle holds here, consider that the smallest angle ( ${\theta }_{\text{1}}$ in the example) is for the maximum value of $m_l=0$ , namely $m_l=l$ . For that smallest angle,

which approaches 1 as $l$ becomes very large. If $\text{cos}\theta =1$ , then $\theta =\mathrm{0º}$ . Furthermore, for large $l$ , there are many values of $m_l$ , so that all angles become possible as $l$ gets very large.