6.2 Discovery of the parts of the atom: electrons and nuclei  (Page 3/7)

An American physicist, Robert Millikan (1868–1953) (see [link] ), decided to improve upon Thomson’s experiment for measuring $q_e$ and was eventually forced to try another approach, which is now a classic experiment performed by students. The Millikan oil drop experiment is shown in [link] .

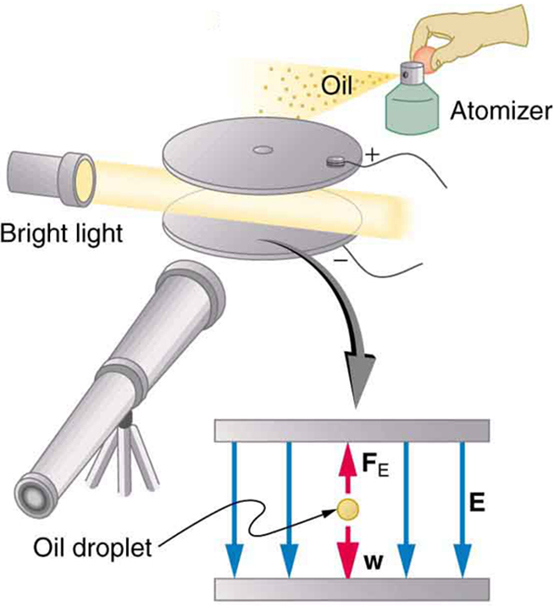
In the Millikan oil drop experiment, fine drops of oil are sprayed from an atomizer. Some of these are charged by the process and can then be suspended between metal plates by a voltage between the plates. In this situation, the weight of the drop is balanced by the electric force:

The electric field is produced by the applied voltage, hence, $E=V/d$ , and $V$ is adjusted to just balance the drop’s weight. The drops can be seen as points of reflected light using a microscope, but they are too small to directly measure their size and mass. The mass of the drop is determined by observing how fast it falls when the voltage is turned off. Since air resistance is very significant for these submicroscopic drops, the more massive drops fall faster than the less massive, and sophisticated sedimentation calculations can reveal their mass. Oil is used rather than water, because it does not readily evaporate, and so mass is nearly constant. Once the mass of the drop is known, the charge of the electron is given by rearranging the previous equation:

where $d$ is the separation of the plates and $V$ is the voltage that holds the drop motionless. (The same drop can be observed for several hours to see that it really is motionless.) By 1913 Millikan had measured the charge of the electron $q_e$ to an accuracy of 1%, and he improved this by a factor of 10 within a few years to a value of $-1\text{.}\text{60}\times {\text{10}}^{-\text{19}}\text{C}$ . He also observed that all charges were multiples of the basic electron charge and that sudden changes could occur in which electrons were added or removed from the drops. For this very fundamental direct measurement of $q_e$ and for his studies of the photoelectric effect, Millikan was awarded the 1923 Nobel Prize in Physics.

With the charge of the electron known and the charge-to-mass ratio known, the electron’s mass can be calculated. It is

Substituting known values yields

or

where the round-off errors have been corrected. The mass of the electron has been verified in many subsequent experiments and is now known to an accuracy of better than one part in one million. It is an incredibly small mass and remains the smallest known mass of any particle that has mass. (Some particles, such as photons, are massless and cannot be brought to rest, but travel at the speed of light.) A similar calculation gives the masses of other particles, including the proton. To three digits, the mass of the proton is now known to be