6.2 Discovery of the parts of the atom: electrons and nuclei  (Page 2/7)

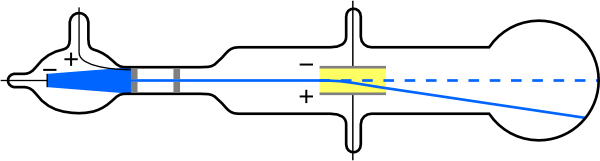
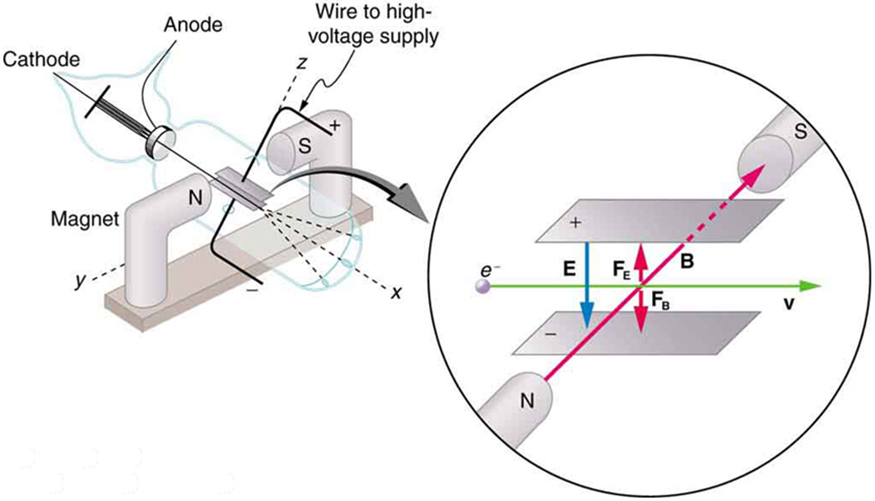
To see how the amount of deflection is used to calculate $q_e/m_e$ , note that the deflection is proportional to the electric force on the electron:

But the vertical deflection is also related to the electron’s mass, since the electron’s acceleration is

The value of $F$ is not known, since $q_e$ was not yet known. Substituting the expression for electric force into the expression for acceleration yields

Gathering terms, we have

The deflection is analyzed to get $a$ , and $E$ is determined from the applied voltage and distance between the plates; thus, $\frac{q_e}{m_e}$ can be determined. With the velocity known, another measurement of $\frac{q_e}{m_e}$ can be obtained by bending the beam of electrons with the magnetic field. Since $F_{\text{mag}}=q_e\text{vB}=m_{e}a$ , we have $q_e/m_e=a/\text{vB}$ . Consistent results are obtained using magnetic deflection.

What is so important about $q_e/m_e$ , the ratio of the electron’s charge to its mass? The value obtained is

This is a huge number, as Thomson realized, and it implies that the electron has a very small mass. It was known from electroplating that about ${\text{10}}^8\text{C/kg}$ is needed to plate a material, a factor of about 1000 less than the charge per kilogram of electrons. Thomson went on to do the same experiment for positively charged hydrogen ions (now known to be bare protons) and found a charge per kilogram about 1000 times smaller than that for the electron, implying that the proton is about 1000 times more massive than the electron. Today, we know more precisely that

where $q_p$ is the charge of the proton and $m_p$ is its mass. This ratio (to four significant figures) is 1836 times less charge per kilogram than for the electron. Since the charges of electrons and protons are equal in magnitude, this implies $m_p=\text{1836}{m}_e$ .

Thomson performed a variety of experiments using differing gases in discharge tubes and employing other methods, such as the photoelectric effect, for freeing electrons from atoms. He always found the same properties for the electron, proving it to be an independent particle. For his work, the important pieces of which he began to publish in 1897, Thomson was awarded the 1906 Nobel Prize in Physics. In retrospect, it is difficult to appreciate how astonishing it was to find that the atom has a substructure. Thomson himself said, “It was only when I was convinced that the experiment left no escape from it that I published my belief in the existence of bodies smaller than atoms.”

Thomson attempted to measure the charge of individual electrons, but his method could determine its charge only to the order of magnitude expected.

Since Faraday’s experiments with electroplating in the 1830s, it had been known that about 100,000 C per mole was needed to plate singly ionized ions. Dividing this by the number of ions per mole (that is, by Avogadro’s number), which was approximately known, the charge per ion was calculated to be about $1\text{.}6\times {\text{10}}^{-\text{19}}\text{C}$ , close to the actual value.