| << Chapter < Page | Chapter >> Page > |
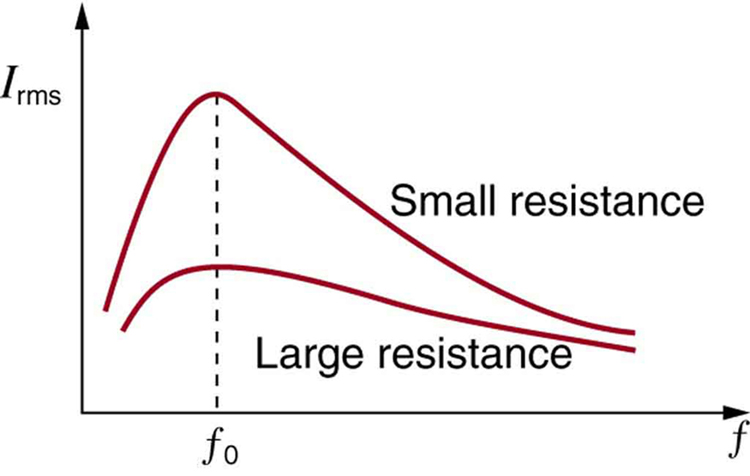
Resonance in AC circuits is analogous to mechanical resonance, where resonance is defined to be a forced oscillation—in this case, forced by the voltage source—at the natural frequency of the system. The receiver in a radio is an RLC circuit that oscillates best at its . A variable capacitor is often used to adjust to receive a desired frequency and to reject others. [link] is a graph of current as a function of frequency, illustrating a resonant peak in at . The two curves are for two different circuits, which differ only in the amount of resistance in them. The peak is lower and broader for the higher-resistance circuit. Thus the higher-resistance circuit does not resonate as strongly and would not be as selective in a radio receiver, for example.
For the same RLC series circuit having a resistor, a 3.00 mH inductor, and a capacitor: (a) Find the resonant frequency. (b) Calculate at resonance if is 120 V.
Strategy
The resonant frequency is found by using the expression in . The current at that frequency is the same as if the resistor alone were in the circuit.
Solution for (a)
Entering the given values for and into the expression given for in yields
Discussion for (a)
We see that the resonant frequency is between 60.0 Hz and 10.0 kHz, the two frequencies chosen in earlier examples. This was to be expected, since the capacitor dominated at the low frequency and the inductor dominated at the high frequency. Their effects are the same at this intermediate frequency.
Solution for (b)
The current is given by Ohm’s law. At resonance, the two reactances are equal and cancel, so that the impedance equals the resistance alone. Thus,
Discussion for (b)
At resonance, the current is greater than at the higher and lower frequencies considered for the same circuit in the preceding example.
If current varies with frequency in an RLC circuit, then the power delivered to it also varies with frequency. But the average power is not simply current times voltage, as it is in purely resistive circuits. As was seen in [link] , voltage and current are out of phase in an RLC circuit. There is a phase angle between the source voltage and the current , which can be found from
For example, at the resonant frequency or in a purely resistive circuit , so that . This implies that and that voltage and current are in phase, as expected for resistors. At other frequencies, average power is less than at resonance. This is both because voltage and current are out of phase and because is lower. The fact that source voltage and current are out of phase affects the power delivered to the circuit. It can be shown that the average power is

Notification Switch
Would you like to follow the 'College physics ii' conversation and receive update notifications?