1. Home
  2. Basic physics for medical imaging
  3. Introduction to quantum physics
  4. Photon momentum

5.4 Photon momentum  (Page 3/5)

<< Chapter < Page
  Basic physics for medical imaging     Page 3 / 5
Chapter >> Page >
(a) A payload having an umbrella-shaped solar sail attached to it is shown. The direction of movement of payload and direction of incident photons are shown using arrows. (b) A photograph of the top view of a silvery space sail.
(a) Space sails have been proposed that use the momentum of sunlight reflecting from gigantic low-mass sails to propel spacecraft about the solar system. A Russian test model of this (the Cosmos 1) was launched in 2005, but did not make it into orbit due to a rocket failure. (b) A U.S. version of this, labeled LightSail-1, is scheduled for trial launches in the first part of this decade. It will have a 40-m 2 sail. (credit: Kim Newton/NASA)

Relativistic photon momentum

There is a relationship between photon momentum p size 12{p} {} and photon energy E size 12{E} {} that is consistent with the relation given previously for the relativistic total energy of a particle as E 2 = ( pc ) 2 + ( mc ) 2 size 12{E rSup { size 8{2} } = \( ital "pc" \) rSup { size 8{2} } + \( ital "mc" \) rSup { size 8{2} } } {} . We know m size 12{m} {} is zero for a photon, but p size 12{p} {} is not, so that E 2 = ( pc ) 2 + ( mc ) 2 size 12{E rSup { size 8{2} } = \( ital "pc" \) rSup { size 8{2} } + \( ital "mc" \) rSup { size 8{2} } } {} becomes

E = pc , size 12{E = ital "pc"} {}

or

p = E c (photons). size 12{p = { {E} over {c} } } {}

To check the validity of this relation, note that E = hc / λ size 12{E = ital "hc"/λ} {} for a photon. Substituting this into p = E / c size 12{p = E"/c"} {} yields

p = hc / λ / c = h λ , size 12{p = left ( ital "hc"/λ right )/c = { {h} over {λ} } } {}

as determined experimentally and discussed above. Thus, p = E / c size 12{p = E"/c"} {} is equivalent to Compton’s result p = h / λ size 12{p = h/λ} {} . For a further verification of the relationship between photon energy and momentum, see [link] .

Photon detectors

Almost all detection systems talked about thus far—eyes, photographic plates, photomultiplier tubes in microscopes, and CCD cameras—rely on particle-like properties of photons interacting with a sensitive area. A change is caused and either the change is cascaded or zillions of points are recorded to form an image we detect. These detectors are used in biomedical imaging systems, and there is ongoing research into improving the efficiency of receiving photons, particularly by cooling detection systems and reducing thermal effects.

Photon energy and momentum

Show that p = E / c size 12{p = E"/c"} {} for the photon considered in the [link] .

Strategy

We will take the energy E size 12{E} {} found in [link] , divide it by the speed of light, and see if the same momentum is obtained as before.

Solution

Given that the energy of the photon is 2.48 eV and converting this to joules, we get

p = E c = ( 2.48 eV ) ( 1 . 60 × 10 –19 J/eV ) 3 . 00 × 10 8 m/s = 1 . 33 × 10 –27 kg ⋅ m/s . size 12{p = { {E} over {c} } = { { \( 2 "." "48 eV" \) \( 1 "." "60 " times " 10" rSup { size 8{"–19"} } " J/eV" \) } over {3 "." "00 " times " 10" rSup { size 8{8} } " m/s"} } =" 1" "." "33 " times " 10" rSup { size 8{"–27"} } " kg " cdot " m/s"} {}

Discussion

This value for momentum is the same as found before (note that unrounded values are used in all calculations to avoid even small rounding errors), an expected verification of the relationship p = E / c size 12{p = E"/c"} {} . This also means the relationship between energy, momentum, and mass given by E 2 = ( pc ) 2 + ( mc ) 2 size 12{E rSup { size 8{2} } = \( ital "pc" \) rSup { size 8{2} } + \( ital "mc" \) rSup { size 8{2} } } {} applies to both matter and photons. Once again, note that p size 12{p} {} is not zero, even when m size 12{m} {} is.

Problem-solving suggestion

Note that the forms of the constants h = 4 . 14 × 10 –15 eV ⋅ s size 12{h =" 4" "." "14 " times " 10" rSup { size 8{"–15"} } " eV " cdot " s"} {} and hc = 1240 eV ⋅ nm size 12{ ital "hc" =" 1240 eV " cdot " nm"} {} may be particularly useful for this section’s Problems and Exercises.

Section summary

  • Photons have momentum, given by p = h λ size 12{p = { {h} over {λ} } } {} , where λ size 12{λ} {} is the photon wavelength.
  • Photon energy and momentum are related by p = E c size 12{p = { {E} over {c} } } {} , where E = hf = hc / λ size 12{E = ital "hf"= ital "hc"/λ } {} for a photon.

Conceptual questions

Which formula may be used for the momentum of all particles, with or without mass?

Is there any measurable difference between the momentum of a photon and the momentum of matter?

Why don’t we feel the momentum of sunlight when we are on the beach?

Problems&Exercises

(a) Find the momentum of a 4.00-cm-wavelength microwave photon. (b) Discuss why you expect the answer to (a) to be very small.

(a) 1.66 × 10 − 32 kg ⋅ m/s size 12{1 "." "66" times "10" rSup { size 8{ - "32"} } `"kg" cdot "m/s"} {}

(b) The wavelength of microwave photons is large, so the momentum they carry is very small.

(a) What is the momentum of a 0.0100-nm-wavelength photon that could detect details of an atom? (b) What is its energy in MeV?

(a) What is the wavelength of a photon that has a momentum of 5 . 00 × 10 − 29 kg ⋅ m/s size 12{5 "." "00" times "10" rSup { size 8{ - "29"} } `"kg" cdot "m/s"} {} ? (b) Find its energy in eV.

(a) 13.3 μm

(b) 9 . 38 × 10 -2 eV

(a) A γ size 12{γ} {} -ray photon has a momentum of 8 . 00 × 10 − 21 kg ⋅ m/s size 12{8 "." "00" times "10" rSup { size 8{ - "21"} } `"kg" cdot "m/s"} {} . What is its wavelength? (b) Calculate its energy in MeV.

(a) Calculate the momentum of a photon having a wavelength of 2 . 50 μm size 12{2 "." "50"" μm"} {} . (b) Find the velocity of an electron having the same momentum. (c) What is the kinetic energy of the electron, and how does it compare with that of the photon?

(a) 2 . 65 × 10 − 28 kg ⋅ m/s size 12{2 "." "65" times "10" rSup { size 8{ - "28"} } `"kg" cdot "m/s"} {}

(b) 291 m/s

(c) electron 3 . 86 × 10 − 26 J size 12{3 "." "86" times "10" rSup { size 8{ - "26"} } " J"} {} , photon 7 . 96 × 10 − 20 J size 12{7 "." "96" times "10" rSup { size 8{ - "20"} } " J"} {} , ratio 2 . 06 × 10 6 size 12{2 "." "06" times "10" rSup { size 8{6} } } {}

Repeat the previous problem for a 10.0-nm-wavelength photon.

(a) Calculate the wavelength of a photon that has the same momentum as a proton moving at 1.00% of the speed of light. (b) What is the energy of the photon in MeV? (c) What is the kinetic energy of the proton in MeV?

(a) 1 . 32 × 10 − 13 m size 12{1 "." "32" times "10" rSup { size 8{ - "13"} } " m"} {}

(b) 9.39 MeV

(c) 4.70 × 10 − 2 MeV size 12{4 "." "70" times "10" rSup { size 8{ - 2} } " MeV"} {}

(a) Find the momentum of a 100-keV x-ray photon. (b) Find the equivalent velocity of a neutron with the same momentum. (c) What is the neutron’s kinetic energy in keV?

Take the ratio of relativistic rest energy, E = γmc 2 mc 2 , to relativistic momentum, p = γ mu size 12{p=γ ital "mu"} {} , and show that in the limit that mass approaches zero, you find E / p = c size 12{E/p=c} {} .

E = γmc 2 mc 2 and P = γmu , so

E P = γmc 2 γmu = c 2 u .

As the mass of particle approaches zero, its velocity u will approach c , so that the ratio of energy to momentum in this limit is

lim m →0 E P = c 2 c = c

which is consistent with the equation for photon energy.

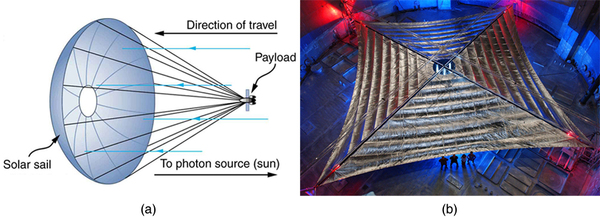
Construct Your Own Problem

Consider a space sail such as mentioned in [link] . Construct a problem in which you calculate the light pressure on the sail in N/m 2 size 12{"N/m" rSup { size 8{2} } } {} produced by reflecting sunlight. Also calculate the force that could be produced and how much effect that would have on a spacecraft. Among the things to be considered are the intensity of sunlight, its average wavelength, the number of photons per square meter this implies, the area of the space sail, and the mass of the system being accelerated.

Unreasonable Results

A car feels a small force due to the light it sends out from its headlights, equal to the momentum of the light divided by the time in which it is emitted. (a) Calculate the power of each headlight, if they exert a total force of 2 . 00 × 10 − 2 N size 12{2 "." "00" times "10" rSup { size 8{ - 2} } " N"} {} backward on the car. (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?

(a) 3 . 00 × 10 6 W size 12{3 "." "00" times "10" rSup { size 8{6} } " W"} {}

(b) Headlights are way too bright.

(c) Force is too large.
<< Chapter < Page Page > Chapter >>
Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Basic physics for medical imaging. OpenStax CNX. Feb 17, 2014 Download for free at http://legacy.cnx.org/content/col11630/1.1
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Basic physics for medical imaging' conversation and receive update notifications?

Ask