| << Chapter < Page | Chapter >> Page > |
Sketch the graph of
Testing for symmetry, we find again that the symmetry tests do not tell the whole story. The graph is not only symmetric with respect to the polar axis, but also with respect to the line and the pole.
Now we will find the zeros. First make the substitution
The zero is The point is on the curve.
Next, we find the maximum We know that the maximum value of when Thus,
The point is on the curve.
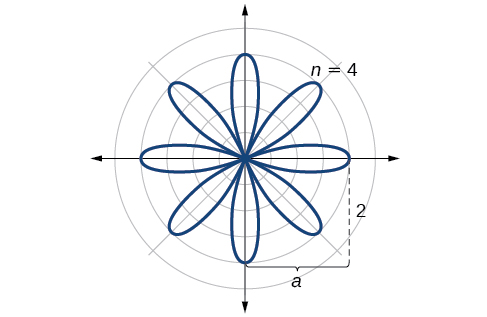
The graph of the rose curve has unique properties, which are revealed in [link] .
| 0 | |||||||
| 2 | 0 | −2 | 0 | 2 | 0 | −2 |
As when it makes sense to divide values in the table by units. A definite pattern emerges. Look at the range of r -values: 2, 0, −2, 0, 2, 0, −2, and so on. This represents the development of the curve one petal at a time. Starting at each petal extends out a distance of and then turns back to zero times for a total of eight petals. See the graph in [link] .
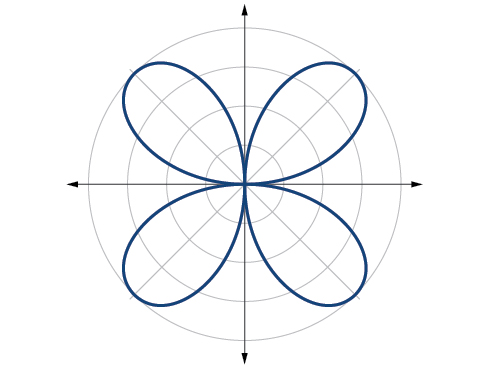
Sketch the graph of
The graph is a rose curve,
even
Sketch the graph of
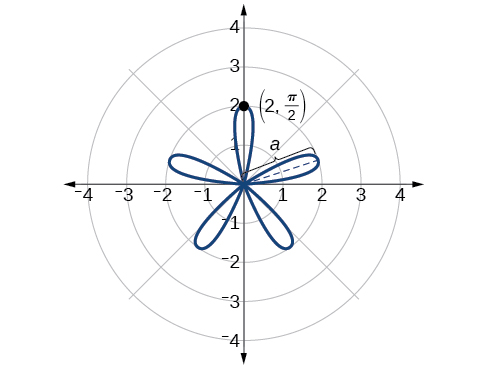
The graph of the equation shows symmetry with respect to the line Next, find the zeros and maximum. We will want to make the substitution
The maximum value is calculated at the angle where is a maximum. Therefore,
Thus, the maximum value of the polar equation is 2. This is the length of each petal. As the curve for odd yields the same number of petals as there will be five petals on the graph. See [link] .
Create a table of values similar to [link] .
| 0 | |||||||
| 0 | 1 | −1.73 | 2 | −1.73 | 1 | 0 |
Sketch the graph of
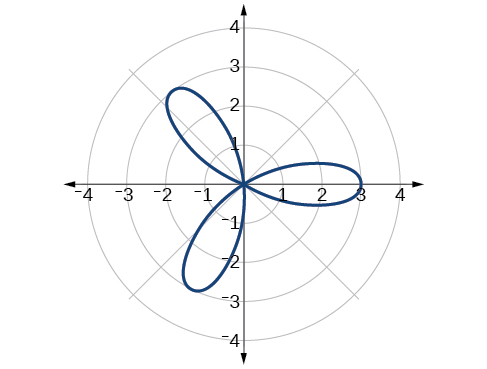
Rose curve, odd
The final polar equation we will discuss is the Archimedes’ spiral, named for its discoverer, the Greek mathematician Archimedes (c. 287 BCE - c. 212 BCE), who is credited with numerous discoveries in the fields of geometry and mechanics.
The formula that generates the graph of the Archimedes’ spiral is given by for As increases, increases at a constant rate in an ever-widening, never-ending, spiraling path. See [link] .
![Two graphs side by side of Archimedes' spiral. (A) is r= theta, [0, 2pi]. (B) is r=theta, [0, 4pi]. Both start at origin and spiral out counterclockwise. The second has two spirals out while the first has one.](/ocw/mirror/col11845_1.2_complete/m49407/CNX_Precalc_Figure_08_04_020new.jpg)
Given an Archimedes’ spiral over sketch the graph.
Sketch the graph of over
As is equal to the plot of the Archimedes’ spiral begins at the pole at the point (0, 0). While the graph hints of symmetry, there is no formal symmetry with regard to passing the symmetry tests. Further, there is no maximum value, unless the domain is restricted.
Create a table such as [link] .
| 0.785 | 1.57 | 3.14 | 4.71 | 5.50 | 6.28 |
Notice that the r -values are just the decimal form of the angle measured in radians. We can see them on a graph in [link] .
![Graph of Archimedes' spiral r=theta over [0,2pi]. Starts at origin and spirals out in one loop counterclockwise. Points (pi/4, pi/4), (pi/2,pi/2), (pi,pi), (5pi/4, 5pi/4), (7pi/4, pi/4), and (2pi, 2pi) are marked.](/ocw/mirror/col11845_1.2_complete/m49407/CNX_Precalc_Figure_08_04_021F.jpg)

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?