3.9 Magnetic fields produced by currents: ampere’s law  (Page 3/12)

Magnetic field produced by a current-carrying solenoid

A solenoid    is a long coil of wire (with many turns or loops, as opposed to a flat loop). Because of its shape, the field inside a solenoid can be very uniform, and also very strong. The field just outside the coils is nearly zero. [link] shows how the field looks and how its direction is given by RHR-2.

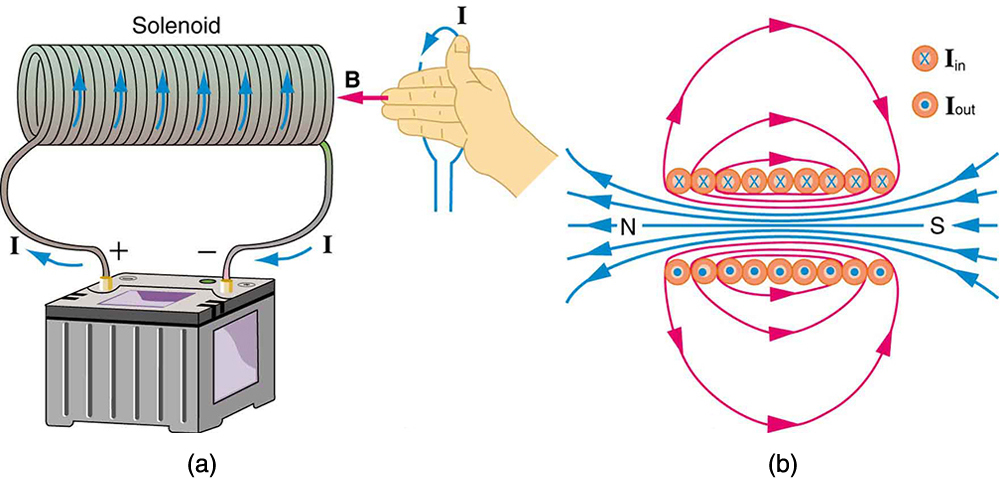
The magnetic field inside of a current-carrying solenoid is very uniform in direction and magnitude. Only near the ends does it begin to weaken and change direction. The field outside has similar complexities to flat loops and bar magnets, but the magnetic field strength inside a solenoid    is simply

where $n$ is the number of loops per unit length of the solenoid $(n=N/l$ , with $N$ being the number of loops and $l$ the length). Note that $B$ is the field strength anywhere in the uniform region of the interior and not just at the center. Large uniform fields spread over a large volume are possible with solenoids, as [link] implies.

There are interesting variations of the flat coil and solenoid. For example, the toroidal coil used to confine the reactive particles in tokamaks is much like a solenoid bent into a circle. The field inside a toroid is very strong but circular. Charged particles travel in circles, following the field lines, and collide with one another, perhaps inducing fusion. But the charged particles do not cross field lines and escape the toroid. A whole range of coil shapes are used to produce all sorts of magnetic field shapes. Adding ferromagnetic materials produces greater field strengths and can have a significant effect on the shape of the field. Ferromagnetic materials tend to trap magnetic fields (the field lines bend into the ferromagnetic material, leaving weaker fields outside it) and are used as shields for devices that are adversely affected by magnetic fields, including the Earth’s magnetic field.

Phet explorations: generator

Generate electricity with a bar magnet! Discover the physics behind the phenomena by exploring magnets and how you can use them to make a bulb light.

Section summary

• The strength of the magnetic field created by current in a long straight wire is given by
  $B=\frac{{\mu }_{0}I}{2\mathrm{\pi r}}(\text{long straight wire}),$
  where $I$ is the current, $r$ is the shortest distance to the wire, and the constant ${\mu }_0=\mathrm{4\pi }\times {\text{10}}^{-7}\text{T}\cdot \text{m/A}$ is the permeability of free space.
• The direction of the magnetic field created by a long straight wire is given by right hand rule 2 (RHR-2): Point the thumb of the right hand in the direction of current, and the fingers curl in the direction of the magnetic field loops created by it.
• The magnetic field created by current following any path is the sum (or integral) of the fields due to segments along the path (magnitude and direction as for a straight wire), resulting in a general relationship between current and field known as Ampere’s law.
• The magnetic field strength at the center of a circular loop is given by
  $B=\frac{{\mu }_{0}I}{2R}(\text{at center of loop}),$
  where $R$ is the radius of the loop. This equation becomes $B={\mu }_0\text{nI}/(2R)$ for a flat coil of $N$ loops. RHR-2 gives the direction of the field about the loop. A long coil is called a solenoid.
• The magnetic field strength inside a solenoid is
  $B={\mu }_0\text{nI}(\text{inside a solenoid}),$
  where $n$ is the number of loops per unit length of the solenoid. The field inside is very uniform in magnitude and direction.

Conceptual questions