| << Chapter < Page | Chapter >> Page > |
For the following exercise, simplify the expression.
For the following exercises, find the exact value.
For the following exercises, find the exact value.
Find and given and is in the interval
Find and given and is in the interval
For the following exercises, use [link] to find the desired quantities.
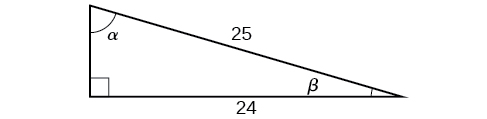
For the following exercises, prove the identity.
For the following exercises, rewrite the expression with no powers.
For the following exercises, evaluate the product for the given expression using a sum or difference of two functions. Write the exact answer.
For the following exercises, evaluate the sum by using a product formula. Write the exact answer.
For the following exercises, change the functions from a product to a sum or a sum to a product.
For the following exercises, find all exact solutions on the interval
For the following exercises, find all exact solutions on the interval
No solution
For the following exercises, simplify the equation algebraically as much as possible. Then use a calculator to find the solutions on the interval Round to four decimal places.
For the following exercises, graph each side of the equation to find the zeroes on the interval
For the following exercises, graph the points and find a possible formula for the trigonometric values in the given table.
A man with his eye level 6 feet above the ground is standing 3 feet away from the base of a 15-foot vertical ladder. If he looks to the top of the ladder, at what angle above horizontal is he looking?
Using the ladder from the previous exercise, if a 6-foot-tall construction worker standing at the top of the ladder looks down at the feet of the man standing at the bottom, what angle from the horizontal is he looking?

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?